Four Golden Circles

Bùi Quang Tuån has posted on the CutTheKnotMath facebook page a configuration of four circles and a parallelogram rich in interrelations between the parts among which are several sightings of the Golden Ratio.

Main statement

Each of the four congruent circles $(A),$ $(B),$ $(C),$ $(D)$ touches other two and passes through the center of the remaining third, as shown:

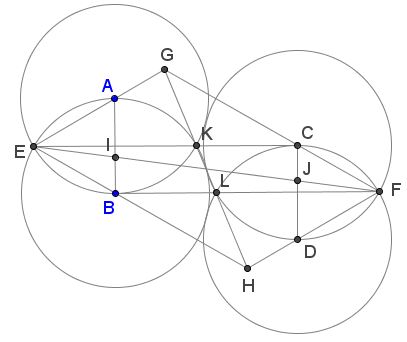
four golden circles by Quang Tuan Bui

In the parallelogram $EHFG,$

The sides are in Golden Ratio: $FG/EG=\phi,$
The diagonals are in Golden Ratio: $EF/GH=\phi,$
Circle centers divide the sides in Golden Ratio, e.g., $AE/AG=BE/BH=\phi,$
The two center lines $AB$ and $CD$ are divided in Golden Ratio by the diagonal $EF,$ e.g. $AI/BI=\phi,$
Two lines $BF$ and $CE$ are divided in Golden Ratio by the diagonal $GH,$ e.g. $EK/CK=\phi,$
In turn, lines $BF$ and $CE$ divide the diagonal $GH$ in Golden Ratio, e.g., $GL/HL=\phi.$

Note: The configuration has several additional properties worth of consideration. These are listed at the bottom of the page.

Proof

Without loss of generality, assume that the common radius of the four circles is $1.$ Let $N$ be the second intersection of $(A)$ and $(B);$ $M$ the midpoint of $AB.$

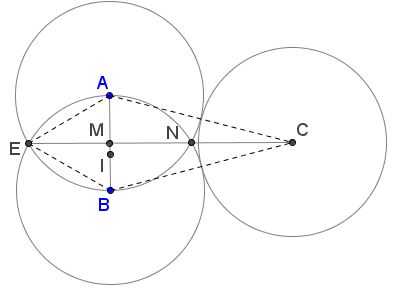
four golden circles by Quang Tuan Bui, step 1

Due to the symmetry of the configuration, $M$ is the intersection of $AB$ and $CE,$ $\Delta ABC$ is isosceles, with $AB=1,$ $AC=BC=2.$ By the Pythagorean theorem, $CM=\sqrt{15}/2.$ In equilateral $\Delta ABE,$ sides are equal to $1$ so that $EM = \sqrt{3}/2.$ By symmetry, also $MN=\sqrt{3}/2.$ Thus

$\displaystyle CE=\frac{\sqrt{15}}{2}+\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2}(\sqrt{5}+1)$

and $\displaystyle\frac{CE}{EN}=\frac{\sqrt{5}+1}{2}=\phi.$

Let now $I$ and $J$ be the intersections of $EF$ with $AB$ and $CD,$ respectively. By symmetry, $AI=DJ,$ $BI=CJ.$

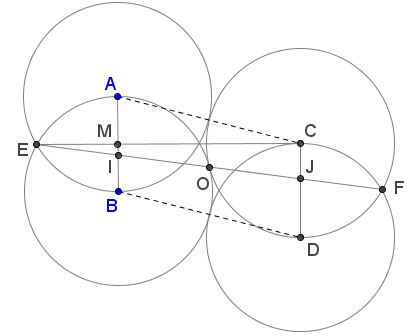
four golden circles by Quang Tuan Bui, step 2

Triangles $CEJ$ and $MEI$ are similar so that $CE/EM=CJ/MI.$ From the foregoing discussion, $CE/EM=\sqrt{5}+1.$ Let $CJ=BI=x.$ Then $\displaystyle MI=\frac{1}{2}-x,$ giving an equation:

$\displaystyle\frac{x}{\frac{1}{2}-x}=\sqrt{5}+1,$

solving which we get $\displaystyle BI=x=\frac{3-\sqrt{5}}{2}.$ Now, $\displaystyle AI=1-x=\frac{\sqrt{5}-1}{2}$ and, as can be easily verified, $\displaystyle\frac{AI}{BI}=\phi.$ This proves #4.

Further, $\angle BEA=60^{\circ}$ so $\angle EGC=\angle EGF=120^{\circ}.$

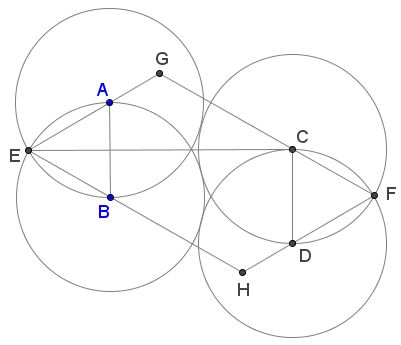
four golden circles by Quang Tuan Bui, step 3

$\Delta EGC$ is isosceles, with $\angle CEG=30^{\circ},$ implying

$\begin{align}\displaystyle EG &=\frac{\frac{1}{2}CE}{\cos 30^{\circ}}\\ &=\frac{1}{2}\cdot \frac{\sqrt{3}}{2}(\sqrt{5}+1)\cdot\frac{2}{\sqrt{3}}\\ &=\frac{\sqrt{5}+1}{2}=\phi. \end{align}$

$FG=GC+CF=\phi +1=\phi^{2}$ such that $FG/EG=FG/CG=\phi,$ proving #1. We now possess all segment lengths to verify #3 directly.

The validity of #4 is the subject of the following

Lemma

In a parallelogram $EHFG$ with angles of $60^{\circ}$ and $120^{\circ},$ if the sides relate in the Golden Ratio, so do the diagonals.

Proof

Using coordinates makes a 1-step proof.

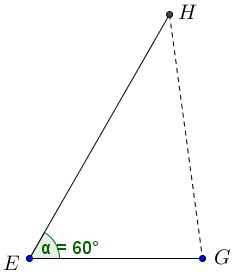
four golden circles by Quang Tuan Bui, step 4

Let $E$ be the origin, $G=(1,0),$ $EH=\phi,$ and $\angle GEH=60^{\circ}.$ Then $\displaystyle H=\bigg(\frac{\phi}{2},\frac{\phi\sqrt{3}}{2}\bigg),$ implying

$\begin{align}\displaystyle GH^{2}&=\bigg(1-\frac{\phi}{2}\bigg)^{2}+\bigg(\frac{\phi\sqrt{3}}{2}\bigg)^{2}\\ &=1-\phi+\frac{\phi^{2}}{4}+\frac{3\phi^{2}}{4}\\ &=1-\phi+\phi^{2}\\ &=(1-\phi)+(1+\phi)=2. \end{align}$

Similarly, $EF^{2}=(1+\phi)+(1+\phi)=2(1+\phi)=2\phi^{2},$ so that $EF/GH=\phi.$

Note: In addition to #5 and #6, the diagram has several attractive properties (similar triangles, point collinearity, line concurrency, one angle being twice another, the angles between the diagonals being $60^{\circ}/120^{\circ},$ etc.) discovering which, along with proving #5 and $6 is left to the reader.

Golden Ratio

49552023