Golden Ratio as a Mathematical Morsel

Here's another construction of the Golden Ratio posted by Tran Quang Hung at the CutTheKnotMath facebook page.

Square $MNPQ$ is inscribed into square $ABCD$ so that the lines joining their vertices intersect the sides of $MNPQ$ at the midpoints $X,Y,Z,W,$ as shown:

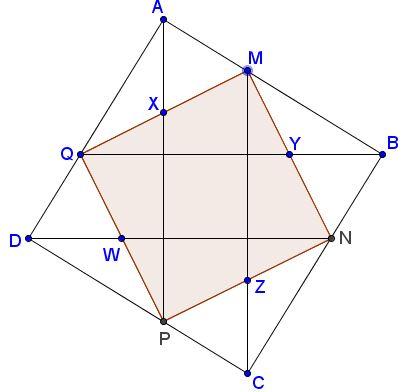
golden ratio by Tran Quang Hung, construction #6, statement

Prove that the vertices of $MNPQ$ divide the sides of $ABCD$ in the Golden Ratio, e.g. $\displaystyle\frac{BM}{AM}=\phi.$

Construction

This is how square $MNPQ$ can be inscribed into square $ABCD$ as required in the statement. The construction is backwards, starting with square $MNPQ.$ Erect semicircles on its sides and draw the lines through the vertices and the midpoints, e.g., $MZ,$ till they intersect the semicircles:

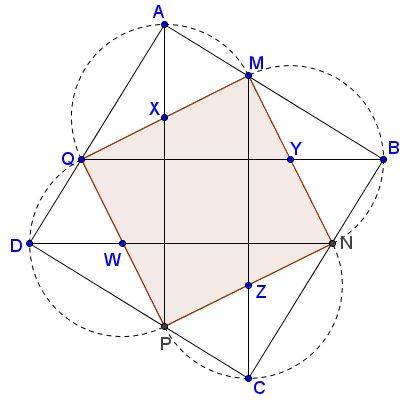
golden ratio by Tran Quang Hung, construction #6, construction

The intersections form square $ABCD.$

Proof

I find it convenient to add a third square - $FGHI$ - to the diagram, and designate the small one that is already present as $RSTU:$

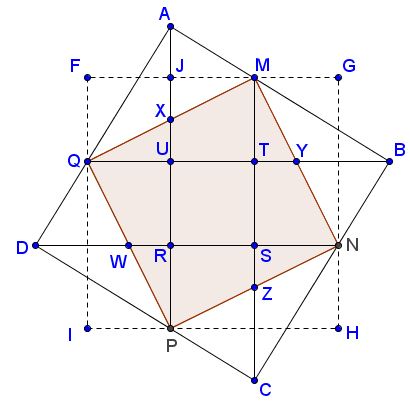
golden ratio by Tran Quang Hung, construction #6, proof

These squares made an appearance early at the site development as an example of a simple math curiosity - mathematical morsels, as I referred to them at the time. $FGHI$ is being cut into 9 copies of $RSTU.$

Let the side of the smallest square be $2:$ $RS=\ldots =2.$ Then $MS=4,$ $SN=2,$ and $MN=2\sqrt{5}.$ Since $Y$ is the circumcenter of the right triangle $MNB,$ $BY=\sqrt{5},$ so that $BT=\sqrt{5}+1.$ In triangle $BTM,$

$BM^{2}=(\sqrt{5}+1)^{2}+2^{2}=2\sqrt{5}(\sqrt{5}+1).$

Similarly, in triangle $AMJ,$ $MJ=2,$ $AJ=\sqrt{5}-1,$ such that

$AM^{2}=(\sqrt{5}-1)^{2}+2^{2}=2\sqrt{5}(\sqrt{5}-1).$

Thus we get

$\displaystyle\frac{BM^{2}}{AM^{2}}=\frac{\sqrt{5}+1}{\sqrt{5}-1}=\frac{\sqrt{5}+3}{2}=1+\phi=\phi^{2},$

just as required.

Golden Ratio

71573679