Golden Ratio in Equilateral Triangle on the Shoulders of George Odom
Source
The following has been posted by Kadir Altintas at the Peru Geometrico facebook group.
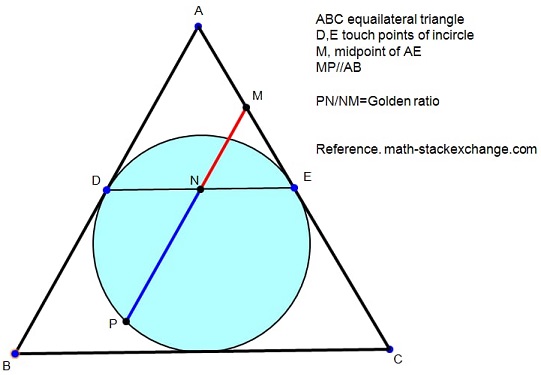
Problem
$ABC$ is an equilateral triangle; $D,F$ are intagent points on $AB,AC$ respectively; $N$ is the midpoint of $DE;$ $MP$ through $N$ is parallel to $AB$ where $M$ is on $AC,$ $P$ is on the incircle of $\Delta ABC,$ so that $N$ is in the segment $MP.$
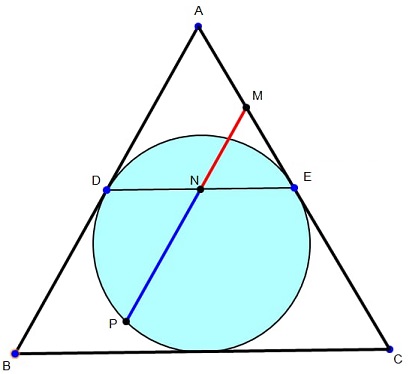
Prove that $\displaystyle \frac{PN}{NM}=\varphi,$ the Golden Ratio.
Proof
Let $G=MP\cap DF,$ where $F$ is the midpoint of $BC.$ Since $N$ is the midpoint of $DE,$ the two equilateral triangles $MNE$ and $DGN$ are equal.
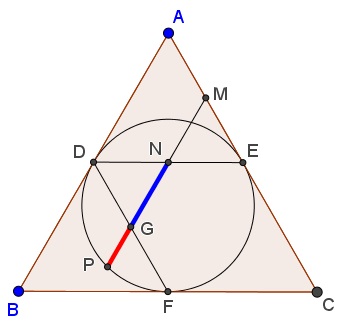
This was one of the first and most surprising discoveries in modern era made by George Odom in the early 1980s that $\displaystyle \frac{NG}{PG}=\varphi.$ It follows that
$\displaystyle\begin{align} \frac{PN}{NM}&=\frac{PG+GN}{GN}=\frac{PG}{GN}+1=\frac{1}{\varphi}+1\\ &=\frac{\varphi+1}{\varphi}=\frac{\varphi^2}{\varphi}=\varphi. \end{align}$
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73580518
