Golden Ratio with a Rusty Compass

In a 2005 article, K. Hofstetter, offered an elegant way of constructing the Golden Ratio with a rusty compass, i.e. a compass whose opening can be set only once.

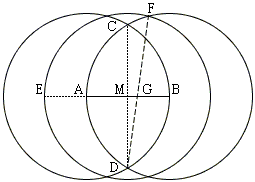
Draw A(B) and B(A) and find C and D at their intersection. Let M be the midpoint of AB found at the intersection of AB and CD. Construct C(M, AB), a circle with center M and radius AB. Let it intersect B(A) in F and another point, F being the farthest from D. Define G as the intersection of AB and DG. G then is the sought point.

The proof is straightforward.

First, BF = FM; so that the projection of F to AB (denoted K) is the midpoint of BM: KM = BK. Right triangles GMD and GKF are similar which gives a proportion:

GM/GK = DM/KF.

It is convenient to assume AB = 4. Then FM = BF = 4, AM = BM = 2, KM = BK = 1. Solving right triangles we obtain KF = √15 and DM = √12 such that GM/GK = 2/√5. Since GM + GK = KM = 1, we derive

GM = 2/(√5 + 2) and GK = 5 - 2√5.

Further, AG = AM + GM = 2(√5 - 1) and BG = GK + BK = 6 - 2√5. Now by direct verification,

AG/BG = (√5 + 1)/2.

References

  1. K. Hofstetter, Division of a Segment in the Golden Section with Ruler and Rusty Compass, Forum Geometricorum, v 5 (2005), pp. 135-136

Fibonacci Numbers

  1. Ceva's Theorem: A Matter of Appreciation
  2. When the Counting Gets Tough, the Tough Count on Mathematics
  3. I. Sharygin's Problem of Criminal Ministers
  4. Single Pile Games
  5. Take-Away Games
  6. Number 8 Is Interesting
  7. Curry's Paradox
  8. A Problem in Checker-Jumping
  9. Fibonacci's Quickies
  10. Fibonacci Numbers in Equilateral Triangle
  11. Binet's Formula by Inducion
  12. Binet's Formula via Generating Functions
  13. Generating Functions from Recurrences
  14. Cassini's Identity
  15. Fibonacci Idendtities with Matrices
  16. GCD of Fibonacci Numbers
  17. Binet's Formula with Cosines
  18. Lame's Theorem - First Application of Fibonacci Numbers

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

72088767