Golden Ratio in Regular Pentagon
The golden ratio, $\phi=\displaystyle\frac{1+\sqrt{5}}{2},$ makes frequent and often unexpected appearance in geometry. Regular pentagon - the pentagram - is one of the places where the golden ratio appears in abundance.
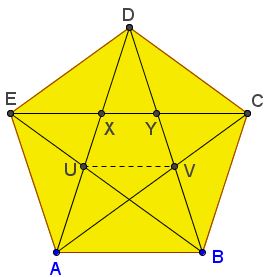
To mention a few (some of which have been proved elsewhere, others are straightforward):
$\displaystyle\frac{DE}{EX}=\frac{EX}{XY}=\frac{UV}{XY}=\frac{EY}{EX}=\frac{BE}{AE}=\phi.$
Most recently Dao Thanh Oai posted an observation at the CutTheKntMath facebook page that in the following diagram $\displaystyle\frac{FB}{FA}=\phi ,$
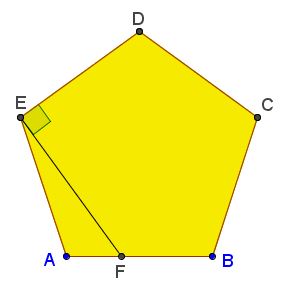
for $EF\perp DE.$ An easy proof is obtained by angle chasing. Observe that $\angle AED=108^{\circ},$ making $\angle AEF=18^{\circ}.$ Now draw $EB.$
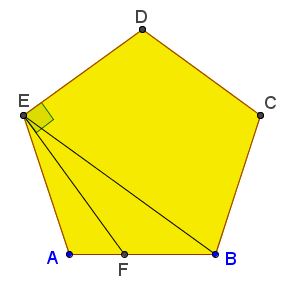
Note that $\angle BEF=18^{\circ}$ also, from which $EF$ is the bisector of $\angle AEB.$ Using the property of angles bisectors, $\displaystyle\frac{BF}{AF}=\frac{BE}{AE}=\phi.$
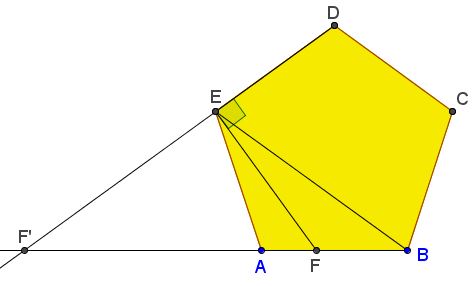
If $F'$ is t he intersection of $DE$ and $AB,$ then also $\displaystyle\frac{BF'}{AF'}=\phi,$ since $EF'$ is the external angle bisector in $\Delta ABE.$
Further, there are multiple additional occurences of the Golden Ratio. For example, in the diagram
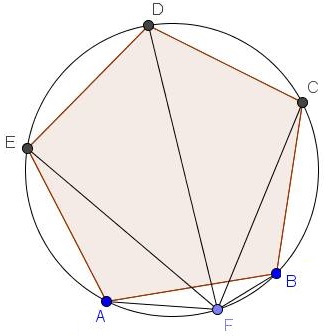
we have
$\displaystyle\frac{EF+CF}{DF}= \frac{FA + FD}{FE} = \frac{FC - FA}{FB},$
where $F\;$ may very widely.
Tran Quang Hung came up with an overlooked occurence of the Golden Ratio in a regular pentagon:
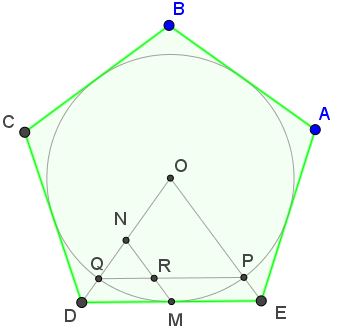
Then, $\displaystyle\frac{ON}{QN}=\frac{PR}{QR}=\varphi.\;$ The details are in a separate page.
Golden Ratio
- Golden Ratio in Geometry
- Golden Ratio in Regular Pentagon
- Golden Ratio in Regular Pentagon
- Golden Ratio in an Irregular Pentagon
- Golden Ratio in a Irregular Pentagon II
- Inflection Points of Fourth Degree Polynomials
- Wythoff's Nim
- Inscribing a regular pentagon in a circle - and proving it
- Cosine of 36 degrees
- Continued Fractions
- Golden Window
- Golden Ratio and the Egyptian Triangle
- Golden Ratio by Compass Only
- Golden Ratio with a Rusty Compass
- From Equilateral Triangle and Square to Golden Ratio
- Golden Ratio and Midpoints
- Golden Section in Two Equilateral Triangles
- Golden Section in Two Equilateral Triangles, II
- Golden Ratio is Irrational
- Triangles with Sides in Geometric Progression
- Golden Ratio in Hexagon
- Golden Ratio in Equilateral Triangles
- Golden Ratio in Square
- Golden Ratio via van Obel's Theorem
- Golden Ratio in Circle - in Droves
- From 3 to Golden Ratio in Semicircle
- Another Golden Ratio in Semicircle
- Golden Ratio in Two Squares
- Golden Ratio in Two Equilateral Triangles
- Golden Ratio As a Mathematical Morsel
- Golden Ratio in Inscribed Equilateral Triangles
- Golden Ratio in a Rhombus
- Golden Ratio in Five Steps
- Between a Cross and a Square
- Four Golden Circles
- Golden Ratio in Mixtilinear Circles
- Golden Ratio With Two Equal Circles And a Line
- Golden Ratio in a Chain of Polygons, So to Speak
- Golden Ratio With Two Unequal Circles And a Line
- Golden Ratio In a 3x3 Square
- Golden Ratio In a 3x3 Square II
- Golden Ratio In Three Tangent Circles
- Golden Ratio In Right Isosceles Triangle
- Golden Ratio Poster
- Golden Ratio Next to the Poster
- Golden Ratio In Rectangles
- Golden Ratio In a 2x2 Square: Without And Within
- Golden Ratio With Two Unequal Circles And a Line II
- Golden Ratio in Equilateral and Right Isosceles Triangles
- Golden Ratio in a Butterfly Astride an Equilateral Triangle
- The Golden Pentacross
- 5-Step Construction of the Golden Ratio, One of Many
- Golden Ratio in 5-gon and 6-gon
- Golden Ratio in an Isosceles Trapezoid with a 60 degrees Angle
- Golden Ratio in Pentagon And Two Squares
- Golden Ratio in Pentagon And Three Triangles
- Golden Ratio in a Mutually Beneficial Relationship
- Star, Six Pentagons and Golden Ratio
- Rotating Square in Search of the Golden Ratio
- Cultivating Regular Pentagons
- Golden Ratio in an Isosceles Trapezoid with a 60 degrees Angle II
- More of Gloden Ratio in Equilateral Triangles
- Golden Ratio in Three Regular Pentagons
- Golden Ratio in Three Regular Pentagons II
- Golden Ratio in Wu Xing
- Golden Ratio In Three Circles And Common Secant
- Flat Probabilities on a Sphere
- Golden Ratio in Square And Circles
- Golden Ratio in Square
- Golden Ratio in Two Squares, Or, Perhaps in Three
- Golden Ratio in Isosceles Triangle
- Golden Ratio in Circles
- Golden Ratio in Isosceles Triangle II
- Golden Ratio in Yin-Yang
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny73577103
