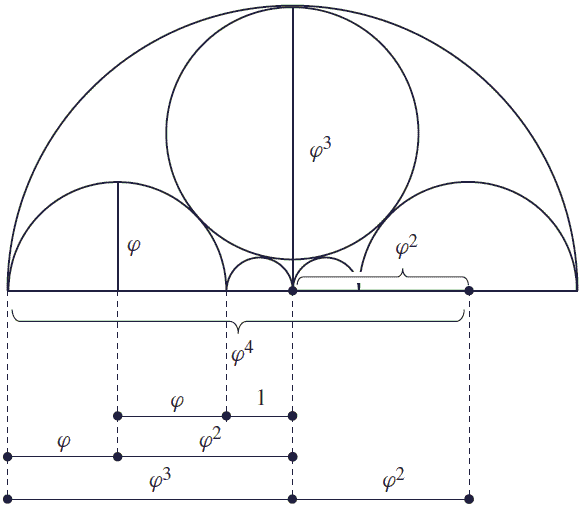
Golden WindowGolden Ratio made multiple appearances at the house of Jerzy Kocik (Golden Window, Math Magazine, 83 (2010) 384-390)) who enjoys a window of a peculiar design. Start with two small central circles of unit diameter. The radius R of the two circles on their left and right, given that a pair of congruent circles (dotted) is simultaneously tangent to all the other circles, is exactly φ. As the diagram below shows various powers of φ, too, pop now and then:
In a two-dimensional configuration with multiple sightings of the golden ratio one would expect to find some occurences of the golden rectangle. Indeed, there are a few in a circular design:
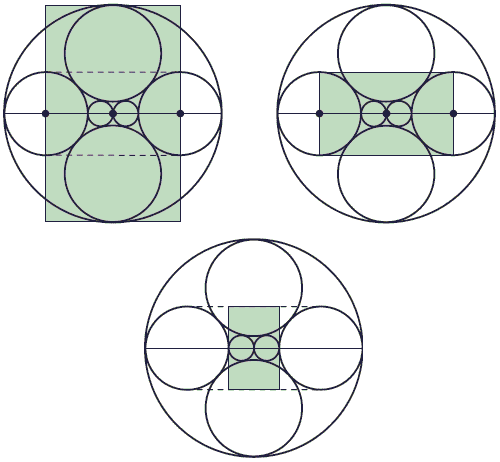
There are several golden rectangles in the semicircular design as well:
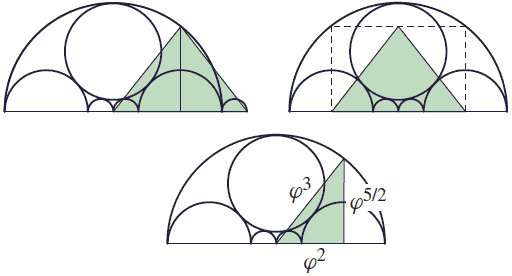
To cap it off, there is an instance of Kepler's triangle:
In addition, two more inscribed circles are perfectly aligned in the configuration:
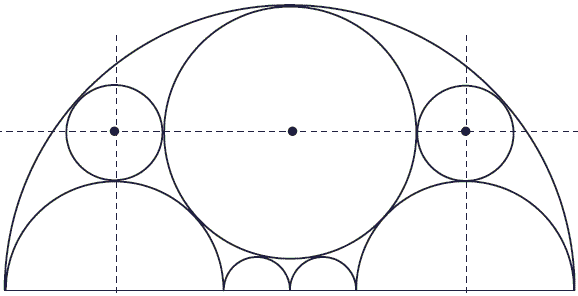
The latter feature could be easily verified. First, with the help of the Pythagorean theorem, we find the radius of the large inscribed circle (the one above the two initial ones) to be 1 + φ - r = (2φ + 1)/(2φ - 1). The vertical alignment imposes another condition: φ + r = φ³ - (2φ + 1)/(2φ - 1). The third condition comes from the new circles being tangent to the big one: (1 + φ)² + (r + φ)² = (φ³ - r)². But, since φ³ = φ×φ² = φ(φ + 1) = φ² + φ = (φ + 1) + φ = 2φ + 1, all three conditions are seen to be actually the same. From either, we get  Fibonacci Numbers
Golden Ratio
|Contact| |Front page| |Contents| |Geometry| |Store| Copyright © 1996-2012 Alexander Bogomolny |
| 41169479 |
