Hippocrates' Squaring of Lunes

The Greeks in the Pythagorean times (6^th-5^th century B.C.) already knew how to square a rectangle, a triangle, and in fact any convex polygon. When squaring the next simplest shape - a circle - appeared a tough problem, squaring other curvilinear figures, like lunes, have been thought of as a natural stepping stone on the way to solving a more difficult problem.

The first and the most famous results on lunes' quadrature have been obtained by a Pythagorean pupil Hippocrates of Chios and reported about a hundred years later by Eudemus of Rhodes in his History of Geometry. Unfortunately the works of both Hippocrates and Eudemus have been long lost. Fortunately, at least part of Eudemus' History has been preserved in a commentary on Aristotle's Physics by Simplicius of Cilicia (6^th century A.D.) In the chapters devoted to the quadrature of lunes he wrote:

What follows is an excerpt from Simpilicius' commentary cleared up of his additions by I. Thomas:

The quadratures of lunes, which seemed to belong to an uncommon class of propositions by reason of the close relationship to the circle, were first investigated by Hippocrates, and seemed to be set out in correct form; therefore we shall deal with them at length and go through them. He made his starting point, and set out as the first of the theorems useful to his purpose, that similar segments of circles have the same ratios as the squares on their bases. And this he proved by showing that the squares on the diameters have the same ratios as the circles.

Having first shown this he described in what way it was possible to square a lune whose outer circumference was a semicircle. He did this by circumscribing about a right-angled isosceles triangle a semicircle and about the base a segment of a circle similar to those cut off by the sides. Since the segment about the base is equal to the sum of those about the sides, it follows that when the part of the triangle above the segment about the base is added to both, the lune will be equal to the triangle. Therefore the lune, having been proved equal to the triangle, can be squared. In this way, taking a semicircle as the outer circumference of the lune, Hippocrates readily squared the lune:

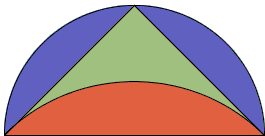
Next in order he assumes an outer circumference greater than a semicircle obtained by constructing a trapezoid having three sides equal to one another while one, the greater of the parallel sides, is such that the square on it is three times the square on each of those sides, and then comprehending the trapezoid in a circle and circumscribing about its greatest side a segment similar to those cut off from the circle by the three equal sides. That the said segment is greater than a semicircle is clear if a diagonal is drawn in the trapezoid. For this diagonal, subtending two sides of the trapezoid, must be such that the square on it is greater than double the square on one of the remaining sides. Therefore the square on BC is greater than double the square on either BA, AC, and therefore also on CD. Therefore the square on BD, the greatest of the sides of the trapezoid, must be less than the sum of the squares on the diagonal and that one of the other sides which is subtended by the said greatest side together with the diagonal. For the squares on BC, CD are greater than three times, and the square on BD is equal to three times, the square on CD. Therefore the angle standing on the greatest side of the trapezoid is acute. Therefore the segment in which it is is greater than a semicircle. And this segment is the outer circumference of the lune.

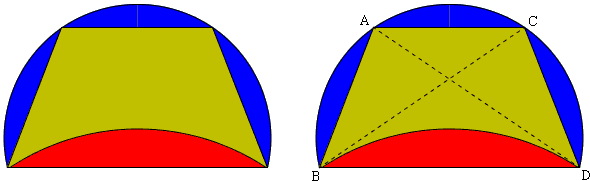
If the outer circumference were less than a semicircle, Hippocrates solved this also, using the following preliminary construction. Let there be a circle with diameter AB and center K. Let CD bisect BK at right angles; and let the straight line EF be placed between this and the circumference verging towards B so that the square on it is one-and-a-half times the square on one of the radii. Let EG be drawn parallel to AB, and from K let straight lines be drawn joining E and F. Let the straight line KF joined to F and produced to meet EG at G, and again let straight lines be drawn from B joining F and G. It is then manifest that EF produced will pass through B - for by hypothesis EF verges towards B - and BG will be equal to EK.

This being so, I say that the trapezoid EKBG can be comprehended in a circle.

Next let a segment of a circle be circumscribed about the triangle EFG; then clearly each of the segments on EF, FG will be similar to the segments on EK, KB, BG.

This being so, the lune so formed, whose outer circumference is EKBG, will be equal to the rectilineal figure composed of the three triangles BFG, BKF, EKF. For the segments cut off from the rectilineal figure, inside the lune, by straight lines EF, FG are together equal to the segments outside the rectilineal figure cut off by EK, KB, BG. For each of the inner segments is one-and-a-half times the square of the radius, that is, the square on EK or KB or BG. Inasmuch then as the lune is made up of the three segments and the rectilineal figure less the two segments - the rectilineal figure including the two segments but not the three - while the sum of the two segments is equal to the sum of the three, it follows that the lune is equal to the rectilineal figure.

Thus Hippocrates squared every lune, seeing that he squared not only the lune which has for its outer circumference a semicircle, but also the lune in which the outer circumference is greater, and that in which it is less, than a semicircle.

Remarks

1. The last sentence in Simplicius' commentary is puzzling. While this is true that Hippocrates did square three kinds of lunes, one for each of the cases where the outer arc is equal to, more than, and less than, the semicircle, the arcs were not random. The selection of the arcs and their constructions give a great credit to the imagination and ingenuity of a mathematician who lived twenty five hundred years ago.

   The abridged versions of the proofs as presented by Simplicius bear some clarification.

   The first case, that of the outer arc being a semicircle, has been treated elsewhere.

   In the second case, the proof may have been shortened if one noticed that from 3AB² = BD², it follows that AB = (4/3)^1/2(BD/2) > BD/2. A trapezoid with base BD and three other sides equal to BD/2 is inscribed in a semicircle. Now that the three smaller sides are greater than BD/2, it takes a larger arc to fit the trapezoid in.

   However, this is a minor point. Simplicius (and apparently Eudemus) in the abridged form that conformed with the ancient practice left out the whole matter of constructing the trapezoid. It's not difficult to find AB to satisfy 3AB² = BD², but assuming the segments AB and BD (AB > BD/2) are given, how one constructs a trapezoid with base BD and three other sides equal to AB? There are several ways to accomplish the feat.

2. The detailed construction in the third case contrasts markedly with the omissions in the second. The latest construction is peculiar, too. As I. Thomas comments [Thomas, p. 244], this is the first example we have had to record of the type of construction known to the Greeks as neuseiz, inclinations or verging. The general problem is to place a straight line so as to verge towards (pass through) a given point and so that a given length is intercepted on it by other lines. (These are the neusis constructions which were applied for angle trisection by Hippocrates himself and Archimedes.)

   Curiously the construction in the third case can be carried out by ruler and compass. From the similarity of triangles BCF and BEA,

   (BF + FE) / BC = AB / BF,

   which leads to a quadratic equation for BF. Quadratic equations are easily solved with ruler and compass. This, in my view, puts the authenticity of the construction in question.

3. Two more squarable lunes have been found in 1771 by L. Euler [Dunham] and, according to M. M. Postnikov [Evolutions], rediscovered by T. Clausen in the 19^th century. In the 20^th century, Russian geometers N. G. Chebotarev (1934) and his student A. V. Dorodnov (1947) showed that these are the only five squarable lunes, thus closing a historic circle of 25 hundred years.

References

1. W. Dunham, Journey Through Genius, Penguin Books, 1990
2. J. Fauvel, J. Gray (eds), The History of Mathematics. A Reader, The Open University, 1987
3. H. O. Midonick (ed), The Treasury of Mathematics, Philosophical Library, 1965
4. A. Shenitzer, J. Stillwells (eds), Mathematical Evolutions, MAA, 2002
5. I. Thomas, Greek Mathematical Works, v1, Harvard University Press, 2006

Quadrature: A Child's Play

• Hippocrates' Squaring of a Lune
• Hippocrates' Squaring of Lunes
• Squaring a Rectangle
• Shearing a Polygon into a Triangle of Equal Area
• Triangle of Equal Area

|Contact| |Front page| |Contents| |Geometry| |Store|

Copyright © 1996-2012 Alexander Bogomolny