cos 36°

The purpose of this page is to establish that

$\cos (36^{\circ}) = \displaystyle\frac{(1 + \sqrt{5})}{4}$.

It's a good exercise in trigonometry that was also useful in solving a curious sangaku problem.

We start with a regular pentagon. As every regular polygon, this one too is cyclic. So that we may assume its vertices lie on a circle and sides and diagonals form inscribed angles.

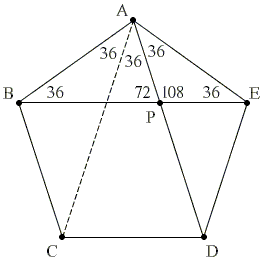
It follows that every angle of the regular pentagon equals $108^{\circ}$. Inscribed $\angle CAD$ is half of the central angle $72^{\circ}=\displaystyle\frac{360^{\circ}}{5}$, i.e.

$\angle CAD = 36^{\circ}$.

By symmetry $\angle BAC = \angle DAE$ implying that these two are also $36^{\circ}$. (Note in passing that we just proved that angle $108^{\circ}$ is trisectable.) Other angles designated in the diagram are also easily calculated.

As far as linear segments are concerned, we may observe that triangles $ABP$, $ABE$, $AEP$ are isosceles, in particular,

$AB = BP$,
$AB = AE$,
$AP = EP$.

Triangles ABE and AEP are also similar, in particular

$BE / AB = AE / EP$, or
$BE\times EP = AB^{2}$, i.e.
$(BP + EP)\times EP = AB^{2}$, and lastly,
$(AB + EP)\times EP = AB^{2}$.

For the ratio $x = AB/EP$ we have the equation

$x + 1 = x^{2}$,

with one positive solution $x = \phi$, the golden ratio. (These calculations were in fact performed to justify a construction of regular pentagon. We return to them here in order to facilitate the references.)

In $\triangle AEP$, $AE = AB$ and $EP$ is one of the sides such that $AE/EP = \phi $. Drop a perpendicular from $P$ to $AE$ to obtain two right triangles. Then say,

$\cos (\angle AEP) = (AE/2)/EP = (AE/EP)/2 = \phi /2$.

But $\angle AEP = 36^{\circ}$ and we get the desired result.

Using $\cos (36^{\circ}) = (1 + \sqrt{5})/4$ we can find

$\cos (18^{\circ})=\sqrt{2(5+\sqrt{5})}/4$

from $\cos 2\alpha = 2\cos ^{2}\alpha - 1$ and then

$\sin (18^{\circ})=\sqrt{2(3-\sqrt{5})}/4$

from $\cos ^{2}\alpha + \sin ^{2}\alpha = 1$. Now, it may be hard to believe but this expression simplifies to

$\sin (18^{\circ}) = (\sqrt{5} - 1)/4$,

which is immediately verified by squaring the two expressions. Also

$\sin (36^{\circ})=\sqrt{2(5-\sqrt{5})}/4$

from $\sin 2\alpha = 2\space \sin \alpha \space \cos \alpha$.

We can easily find $\cos (72^{\circ})$ from $\cos 2\alpha = 2\cos ^{2}\alpha - 1$:

$ \begin{align} \cos (72^{\circ}) &= 2\cos ^{2}(36^{\circ}) - 1 \\ &= 2[(\sqrt{5} + 1) / 4]^{2} - 1 \\ &= (6 + 2\sqrt{5} / 8 - 1 \\ &= (3 + \sqrt{5} / 4 - 1 \\ &= (\sqrt{5} - 1) / 4. \end{align} $

This is of course equal to $\sin (18^{\circ})$ as might have been expected from the general formula, $\sin \alpha = \cos (90^{\circ} - \alpha )$.

And, of course,

$\sin (72^{\circ})=\sqrt{2(5+\sqrt{5})}/4$

because $\sin (72^{\circ}) = \cos (18^{\circ})$.

Finally, let's compute $\sin 54^{\circ}:\;$

$\displaystyle\begin{align} \sin 54^{\circ} &= \sin 36^{\circ}\cos 18^{\circ}+\cos 36^{\circ}\sin 18^{\circ}\\ &= \displaystyle\frac{\sqrt{2(5-\sqrt{5})}}{4}\cdot \displaystyle\frac{\sqrt{2(5+\sqrt{5})}}{4} + \displaystyle\frac{1 + \sqrt{5}}{4}\cdot\displaystyle\frac{\sqrt{5}-1}{4}\\ &=\displaystyle\frac{\sqrt{5}+1}{4}, \end{align}$

as expected since $\sin 54^{\circ}=\cos 36^{\circ}.$

Trigonometry

Fibonacci Numbers

Golden Ratio in Geometry

71862884