Morley's Miracle

In 1899, more than a hundred years ago, Frank Morley, then professor of Mathematics at Haverford College, came across a result so surprising that it entered mathematical folklore under the name of Morley's Miracle. Morley's marvelous theorem states that

The three points of intersection of the adjacent trisectors of the angles of any triangle form an equilateral triangle.

The applet below serves to demonstrate that, indeed, whatever the shape of the given triangle, the Morley triangle is always equilateral.

22 January 2015, Created with GeoGebra

Morley's original proof stemmed from his results on algebraic curves tangent to a given number of lines. As usual in mathematics, numerous attempts have been made to find a simple, elementary proof that could match the level of knowledge and proficiency required to grasp the statement of the theorem. The simplest proofs proceed backwards starting with an equilateral triangle. They differ in subsequent steps. Most such proofs highlight some additional features of the configuration but complicate matters unnecessarily as a few most trivial proofs convincingly demonstrate.

Before giving several backward proofs, here is a direct one which, while logically absolutely transparent, requires some high school trigonometry.

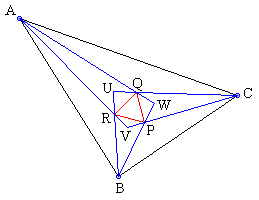
Proof #1

In all likelihood, this proof first appeared in A. Letac, Solution (Morley's triangle), Problem No. 490, Sphinx, 9(1939) 46. I came across it in a Russian book D. O. Shklyarsky, N. N. Chentsov, Y. M. Yaglom, Selected Problems and Theorems of Elementary Mathematics, v. 2, problem 97, Moscow, 1952 and also in The Art of Mathematics by B. Bollobás (Cambridge University Press, 2006, p. 126-127.)

The idea of the proof is fairly straightforward.

  1. In triangles $ARB,$ $BPC,$ $CQA,$ we know the bases - $AB,$ $BC,$ and $AC$ - and the adjacent angles. The Law of Sines then yields the segments $AR,$ $BR,$ $BP,$ $CP,$ $CQ,$ and $AQ.$

  2. Next we apply the Law of Cosines to triangles $AQR,$ $BPR,$ and $CPQ$ to determine (and compare) the segments $QR,$ $PR,$ and $PQ.$ The fact that they come out equal proves the theorem.

For simplicity, let (angles) $A = 3\alpha,$ $B = 3\beta,$ and $C = 3\gamma.$ This implies that $\alpha + \beta + \gamma = 60^{\circ}.$ Also, assuming that the radius of the circle circumscribed around $\Delta ABC$ equals $1,$ we get $AB = 2\sin (3\gamma),$ $BC = 2\sin (3\alpha),$ $AC = 2\sin (3\beta).$

Consider now $\Delta BPC.$ By the Law of Sines,

$\begin{align}\displaystyle \frac{BP}{\sin (\gamma)} &= \frac{BC}{\sin (180^{\circ} - \beta - \gamma)}\\ &= 2\frac{\sin (3\alpha)}{\sin (\beta + \gamma)}\\ &= 2\frac{\sin (3\alpha)}{\sin (60^{\circ} - \alpha)}. \end{align}$

Therefore, $\displaystyle BP = 2\frac{\sin (3\alpha)\sin (\gamma)}{\sin (60^{\circ} - \alpha)}.$ To simplify the expression note that

$\begin{align} \sin (3\alpha) &= 3\sin (\alpha) - 4\sin^{3}(\alpha)\\ &= 4\sin (\alpha)[(\sqrt{3}/2)^{2} - \sin^{2}(\alpha)]\\ &= 4\sin (\alpha)[\sin^{2}(60^{\circ}) - \sin^{2}(\alpha)]\\ &= 4\sin (\alpha)(\sin (60^{\circ}) + \sin (\alpha))(\sin (60^{\circ}) - \sin (\alpha))\\ &= 4\sin (\alpha) 2\sin[(60^{\circ} + \alpha)/2]\cos[(60^{\circ} - \alpha)/2] 2\sin[(60^{\circ} - \alpha)/2]\cos[(60^{\circ} + \alpha)/2]\\ & = 4\sin (\alpha)\sin (60^{\circ} + \alpha)\sin (60^{\circ} - \alpha). \end{align}$

Reaping the fruits of this effort,

$BP = 8\sin (\alpha)\sin (\gamma)\sin (60^{\circ} + \alpha).$

Similarly,

$BR = 8\sin (\gamma)\sin (\alpha)\sin (60^{\circ} + \gamma).$

There are two ways to proceed to the second step. The traditional one that was employed in the above references invokes the Law of Cosines. A more recent one, due to Leo Giugiuc, makes use of the Law of Sines. I continue with the traditional proof, while Leo's proof deserves to be treated seperately.

We invoke the Law of Cosines in $\Delta BPR:$

$PR^{2} = BP^{2} + BR^{2} - 2 BP\cdot BR \cos (\beta),$

from where

$PR^{2} = 64\sin^{2}(\alpha)\sin^{2}(\gamma)[\sin^{2}(60^{\circ} + \alpha) + \sin^{2}(60^{\circ} + \gamma) - 2\sin (60^{\circ} + \alpha)\sin (60^{\circ} + \gamma)\cos (\beta)].$

Note, however, that $(60^{\circ} + \alpha) + (60^{\circ} + \gamma) + \beta = 180^{\circ}.$ Thus, there exists a triangle with angles $(60^{\circ}+\alpha),$ $(60^{\circ}+\gamma),$ and $\beta.$ Indeed, there is a whole family of similar triangles with those angles. Out of this family, choose the one with the circumscribed radius equal to $1$ (then, as above, by the Law of Sines, its sides have a very simple form.) In that triangle, apply the Law of Cosines:

$\sin^{2}(\beta) = \sin^{2}(60^{\circ} + \alpha) + \sin^{2}(60^{\circ} + \gamma) - 2\sin (60^{\circ} + \alpha)\sin (60^{\circ} + \gamma)\cos (\beta).$

Which gives

$PR = 8\sin (\alpha)\sin (\beta)\sin (\gamma),$

an expression which is symmetric in $\alpha,$ $\beta,$ and $\gamma.$ $QR$ and $PQ$ are similarly found to be equal to the same expression. Therefore, $PR=PQ=QR.$


  • Morley's Miracle

    On Morley and his theorem

    1. Doodling and Miracles
    2. Morley's Pursuit of Incidence
    3. Lines, Circles and Beyond
    4. On Motivation and Understanding
    5. Of Looking and Seeing

    Backward proofs

    1. J.Conway's proof
    2. D. J. Newman's proof
    3. B. Bollobás' proof
    4. G. Zsolt Kiss' proof
    5. Backward Proof by B. Stonebridge
    6. Morley's Equilaterals, Spiridon A. Kuruklis' proof
    7. J. Arioni's Proof of Morley's Theorem

    Trigonometric proofs

    1. Bankoff's proof
    2. B. Bollobás' trigonometric proof
    3. Proof by R. J. Webster
    4. A Vector-based Proof of Morley's Trisector Theorem
    5. L. Giugiuc's Proof of Morley's Theorem
    6. Dijkstra's Proof of Morley's Theorem

    Synthetic proofs

    1. Another proof
    2. Nikos Dergiades' proof
    3. M. T. Naraniengar's proof
    4. An Unexpected Variant
    5. Proof by B. Stonebridge and B. Millar
    6. Proof by B. Stonebridge
    7. Proof by Roger Smyth
    8. Proof by H. D. Grossman
    9. Proof by H. Shutrick
    10. Original Taylor and Marr's Proof of Morley's Theorem
    11. Taylor and Marr's Proof - R. A. Johnson's Version
    12. Morley's Theorem: Second Proof by Roger Smyth
    13. Proof by A. Robson

    Algebraic proofs

    1. Morley's Redux and More, Alain Connes' proof

    Invalid proofs

    1. Bankoff's conundrum
    2. Proof by Nolan L Aljaddou
    3. Morley's Theorem: A Proof That Needs Fixing

    Related material
    Read more...

  • Equilateral and 3-4-5 Triangles
  • Rusty Compass Construction of Equilateral Triangle
  • Equilateral Triangle on Parallel Lines
  • Equilateral Triangle on Parallel Lines II
  • When a Triangle is Equilateral?
  • Viviani's Theorem
  • Viviani's Theorem (PWW)
  • Tony Foster's Proof of Viviani's Theorem
  • Viviani in Isosceles Triangle
  • Viviani by Vectors
  • Slanted Viviani
  • Slanted Viviani, PWW
  • Triangle Classification
  • Napoleon's Theorem
  • Sum of Squares in Equilateral Triangle
  • A Property of Equiangular Polygons
  • Fixed Point in Isosceles and Equilateral Triangles
  • Parallels through the Vertices of Equilateral Triangle

    • |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    • 72354278