Morley's Miracle
A Vector-based Proof

This proof by Cesare Donolato has appeared in Forum Geometricorum, 13 (2013) 233-235.

As in several other proofs, let the angles of $\Delta ABC$ be $3\alpha,$ $3\beta,$ $3\gamma$ so that $\alpha +\beta +\gamma =60^{\circ}.$ The adjacent angle trisectors meet to form Morley's triangle $PQR;$ $BR$ and $CQ$ extended meet at $D.$ Point $P$ is evidently the incenter of $\Delta BDC,$ implying that $DP$ is the bisector of the angle at D.

Lemma

The line $DP$ is perpendicular to the line $RQ.$

Proof of Lemma

Let $\mathbf{e}$ be the unit vector along $DP$ and $\mathbf{s}_1$ the vector representing $QR.$ We need to show that the scalar product $\mathbf{e}\cdot \mathbf{s}_1 =0.$ With a reference to the above diagram, this is equivalent to $(\mathbf{v}_{3}-\mathbf{v}_{2})\cdot\mathbf{e}=0.$

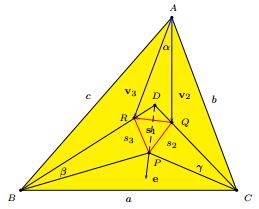
A Vector-based Proof of Morley's Trisector Theorem

In $\Delta BDC,$

$\begin{align} \angle D &= 180^{\circ} - 2\beta -2\gamma\\ &=180^{\circ} - 2(60^{\circ} -\alpha)\\ &=60^{\circ} +2\alpha . \end{align}$

Since $DP$ is the bisector of this angle, $\angle QDP=\angle RDP=30^{\circ}+\alpha.$ By the Exterior Angle Theorem, $\angle AQD=\alpha +\gamma$ and $\angle ARD=\alpha +\beta.$ The angle between vectors $\mathbf{v}_{3}$ and $\mathbf{e},$ being the difference between angles $RDP$ and $ARD,$ is $30^{\circ}-\beta.$ Similarly, the angle between vectors $\mathbf{v}_{2}$ and $\mathbf{e}$ is $30^{\circ}-\gamma.$ If so,

(1)

$\begin{align} (\mathbf{v}_{3}-\mathbf{v}_{2})\cdot\mathbf{e} &= \mathbf{v}_{3}\cdot\mathbf{e}-\mathbf{v}_{2}\cdot\mathbf{e}\\ &=v_{3}\cos (30^{\circ} - \beta)-v_{2}\cos (30^{\circ} - \gamma)\\ &=v_{3}\sin (60^{\circ} + \beta)-v_{2}\sin (60^{\circ} + \gamma). \end{align}$

where $v_{2}$ and $v_{3}$ are the magnitudes of vectors $(\mathbf{v}_{2}$ and $(\mathbf{v}_{3},$ respectively, and can be found with the Law of Sines in triangles $AQC$ and $ARB:$

$\begin{align}\displaystyle v_{2} &= \frac{c\sin\beta}{\sin(\alpha +\beta)}=\frac{c\sin\beta}{\sin(60^{\circ}-\gamma)},\\ v_{3} &= \frac{b\sin\gamma}{\sin(\alpha +\gamma)}=\frac{b\sin\gamma}{\sin(60^{\circ}-\beta)}. \end{align}$

Substituting these into (1) yields

$\begin{align}\displaystyle (\mathbf{v}_{3}-\mathbf{v}_{2})\cdot\mathbf{e} &= \frac{c\sin\beta\sin(60^{\circ}+\beta)}{\sin(60^{\circ}-\gamma)}-\frac{b\sin\gamma\sin(60^{\circ}+\gamma)}{\sin(60^{\circ}-\beta)}\\ &=\frac{c\sin\beta\sin(60^{\circ}+\beta)\sin(60^{\circ}-\beta)-b\sin\gamma\sin(60^{\circ}+\gamma)\sin(60^{\circ}-\gamma)}{\sin(60^{\circ}-\gamma)\sin(60^{\circ}-\beta)}\\ &=\frac{1}{4}\frac{c\sin 3\beta-b\sin 3\gamma}{\sin(60^{\circ}-\gamma)\sin(60^{\circ}-\beta)}, \end{align}$

where we used the identity $\displaystyle\sin x\sin(60^{\circ}-x)\sin(60^{\circ}+x)=\frac{1}{4}\sin 3x.$

But from the Law of sines in $\Delta ABC$ $c\sin 3\beta -b\sin 3\gamma=0,$ $(\mathbf{v}_{3}-\mathbf{v}_{2})\cdot\mathbf{e}=0,$ proving Lemma.

Proof of Morley's Theorem

$DP$ being perpendicular to $RQ,$ it divides the latter in half and $\Delta DQR$ into two congruent right triangles, implying $DQ=DR.$ It follows that triangles $DPQ$ and $DPR$ are also congruent (by SAS), and $s_{2}=s_{3}.$ Similarly, $s_{1}=s_{2},$ and, by transitivity, all three sides of $\Delta PQR$ are equal, completing the proof of Morley's theorem