Slanted Viviani
What Might This Be About?
Source
The problem below grew out from an observation by Miguel Ochoa Sanchez:
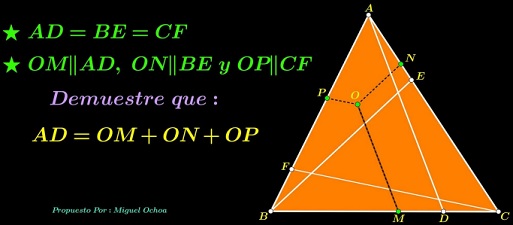
Problem
$ABC$ is an equilateral triangle. Cevians $AD,$ $BE,$ $CF$ are equal (and, for the esthetics' sake, equally inclined to the corresponding sides.) Points $M,N,P$ are on $BC,AC,AB,$ respectively, such that $OM\parallel AD,$ $ON\parallel BE,$ and $OP\parallel CF.$
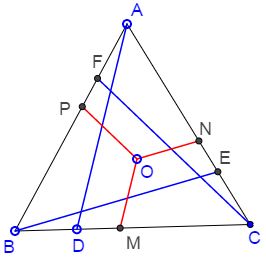
Prove that $OM+ON+OP=AD.$
Proof
Note that, for $AD\perp BC,$ the problem reduces to Viviani's theorem. From here the present statement follows immediately by dropping perpendiculars from $O$ to all three sides and from $A$ to $BC.$ The procedure creates four similar right triangles with the corresponding legs of the three small triangles adding up to the leg of the big one. The same then holds for the hypotenuses of the four triangles.
Viviani's theorem has several proofs at this site. The solution below to the problem at hand does not appear to have an analogue among the included proofs of Viviani's theorem, but is extremely simple and shows that sometimes a generalization of the statement may be proved with the same ease as the statement itself.
If the statement holds for $O$ on a side of $\Delta ABC,$ it holds for any point within the triangle.
This is illustrated by the diagram below:
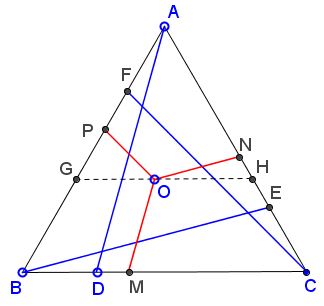
The line through $O$ cuts off, on one hand, an equilateral triangle, and, on the other, a piece of $AD$ equal to $OM.$ Thus $O$ can be chosen on, say, $BC.$
If the statement holds for $O$ at a vertex of $\Delta ABC,$ it holds for any point on a side of the triangle.
This is illustrated by the diagram below:
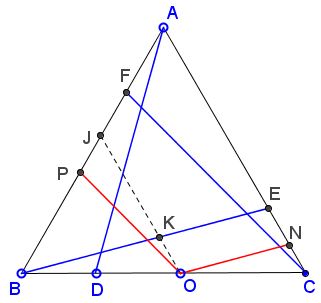
A line through $O$ parallel to $AC$ cuts $BE$ in $K$ and $AB$ in $J.$ Since $ON=KE$ we need only to show that $OP=BK.$ But this is obviously so from the premises of the original problem.
The statement holds for $O$ at a vertex of $\Delta ABC.$
True by the construction.
Acknowledgment
The original statement has been emailed to me by Leo Giugiuc with credits to Miguel Ochoa Sanchez.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73573379
