Morley's Miracle
H. D. Grossman's Proof

Theorem

The three points of intersection of the adjacent trisectors of the angles of any triangle form an equilateral triangle.

Proof

This proof was published in The American Mathematical Monthly, Vol. 50, No. 9 (Nov., 1943), p. 552.

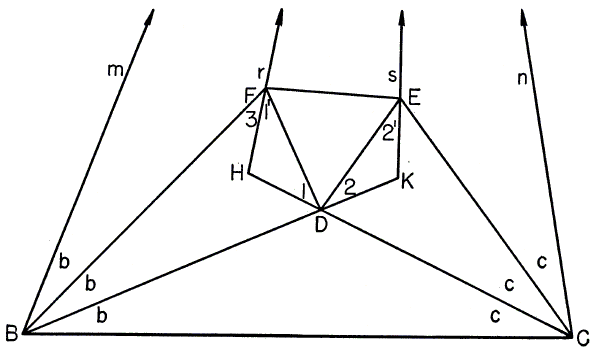
Let the triangle have base BC and angles 3α, 3β,3γ. Let BDK, BF, CDH, CE be angle trisectors. E is determined by making ∠CDE = 60° + β and F by making ∠BDF = 60° + γ. Then

∠EDF = 360° - (180° - β - γ) - (60° + β) - (60° + γ) = 60°.

Also

∠BFD = 180° - (60° + β + γ) = 60° + α.

Similarly, ∠CED = 60° + α.

Grossman's proof of Morley's theorem

Since D is equidistant from BF and CE, DF = DE and ΔDEF is equilateral.

∠1 = (60° + α) - (β - γ) = 60° - β.

Similarly,

∠2 = 60° - γ.

Through F draw line r making ∠1' = ∠1. Through E draw a line s making angle ∠2' = ∠2.

∠3 = (60° + α) - (60° - β) = α + β

and

∠mr = (α + β) - β = α.

Similarly,

∠sn = (α + γ) - γ = α.

Further,

∠mn = (180° - 3β - 3γ) = 3α.

It remains only to prove that the lines m, n, r, and s converge to a point. The line KF joins the vertices of two isosceles triangles and therefore bisects ∠K. Then in triangle mBKs the bisector of ∠ms passes through F and being parallel to r, coincides with it. Similarly in triangle rHCn the bisector of ∠rn passes through E and being parallel to s, coincides with it.


Morley's Miracle

On Morley and his theorem

  1. Doodling and Miracles
  2. Morley's Pursuit of Incidence
  3. Lines, Circles and Beyond
  4. On Motivation and Understanding
  5. Of Looking and Seeing

Backward proofs

  1. J.Conway's proof
  2. D. J. Newman's proof
  3. B. Bollobás' proof
  4. G. Zsolt Kiss' proof
  5. Backward Proof by B. Stonebridge
  6. Morley's Equilaterals, Spiridon A. Kuruklis' proof
  7. J. Arioni's Proof of Morley's Theorem

Trigonometric proofs

  1. Bankoff's proof
  2. B. Bollobás' trigonometric proof
  3. Proof by R. J. Webster
  4. A Vector-based Proof of Morley's Trisector Theorem
  5. L. Giugiuc's Proof of Morley's Theorem
  6. Dijkstra's Proof of Morley's Theorem

Synthetic proofs

  1. Another proof
  2. Nikos Dergiades' proof
  3. M. T. Naraniengar's proof
  4. An Unexpected Variant
  5. Proof by B. Stonebridge and B. Millar
  6. Proof by B. Stonebridge
  7. Proof by Roger Smyth
  8. Proof by H. D. Grossman
  9. Proof by H. Shutrick
  10. Original Taylor and Marr's Proof of Morley's Theorem
  11. Taylor and Marr's Proof - R. A. Johnson's Version
  12. Morley's Theorem: Second Proof by Roger Smyth
  13. Proof by A. Robson

Algebraic proofs

  1. Morley's Redux and More, Alain Connes' proof

Invalid proofs

  1. Bankoff's conundrum
  2. Proof by Nolan L Aljaddou
  3. Morley's Theorem: A Proof That Needs Fixing

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1966-2016 Alexander Bogomolny

72203030