Morley's Miracle
Leo Giugiuc's Proof

The three points of intersection of the adjacent trisectors of the angles of any triangle form an equilateral triangle.

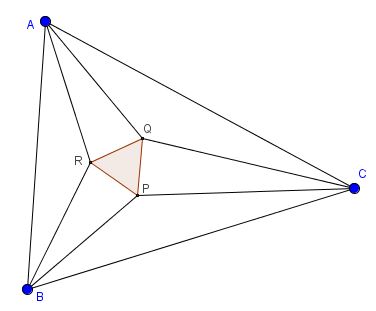
Morley's theorem - statement

In $\Delta QAC,$ we have $\displaystyle\frac{AQ}{\sin\frac{C}{3}}=\frac{AC}{\sin\frac{A+C}{3}};$ but $AC=2R\cdot\sin B,$ where $R$ is the circumradius of $\Delta ABC.$ It follows that

$\displaystyle\frac{AQ}{\sin\frac{C}{3}}=\frac{2R\cdot\sin B}{\sin\frac{A+C}{3}}=8R\cdot\sin\frac{B}{3}\sin\frac{A+C}{3}\sin\frac{\pi +B}{3},.$

implying $\displaystyle AQ=8R\cdot\sin\frac{B}{3}\sin\frac{C}{3}\sin\frac{\pi +C}{3}.$ But the numbers $\displaystyle\frac{A}{3},$ $\displaystyle\frac{\pi +B}{3},$ and $\displaystyle\frac{\pi +C}{3}$ are strictly positive and their sum is $\pi,$ so there is a triangle $XYZ,$ with $\displaystyle X=\frac{A}{3},$ $\displaystyle Y=\frac{\pi +B}{3},$ and $\displaystyle Z=\frac{\pi +C}{3}$ and the circumradius of $\displaystyle\frac{1}{2}.$

In $\Delta XYZ,$ $\displaystyle YZ=\sin\frac{A}{3},$ $\displaystyle XZ=\sin\frac{\pi +B}{3},$ and $\displaystyle XY=\sin\frac{\pi +C}{3};$ but $\displaystyle\frac{AQ}{XZ}=\frac{AR}{XY}=8R\cdot\sin\frac{B}{3}\cdot\sin\frac{C}{3}$ and $\displaystyle\angle QAR=X=\frac{A}{3},$ so that $\Delta AQR$ is similar to $\Delta XZY$ and, therefore, $\displaystyle\frac{QR}{YZ}=8R\cdot\sin\frac{B}{3}\cdot\sin\frac{C}{3}$ which finally gives $\displaystyle QR=8R\cdot\sin\frac{A}{3}\cdot\sin\frac{B}{3}\cdot\sin\frac{C}{3},$ a symmetric function of the angles of $\Delta ABC.$ This leads to $QR=PQ=PR.$


Morley's Miracle

On Morley and his theorem

  1. Doodling and Miracles
  2. Morley's Pursuit of Incidence
  3. Lines, Circles and Beyond
  4. On Motivation and Understanding
  5. Of Looking and Seeing

Backward proofs

  1. J.Conway's proof
  2. D. J. Newman's proof
  3. B. Bollobás' proof
  4. G. Zsolt Kiss' proof
  5. Backward Proof by B. Stonebridge
  6. Morley's Equilaterals, Spiridon A. Kuruklis' proof
  7. J. Arioni's Proof of Morley's Theorem

Trigonometric proofs

  1. Bankoff's proof
  2. B. Bollobás' trigonometric proof
  3. Proof by R. J. Webster
  4. A Vector-based Proof of Morley's Trisector Theorem
  5. L. Giugiuc's Proof of Morley's Theorem
  6. Dijkstra's Proof of Morley's Theorem

Synthetic proofs

  1. Another proof
  2. Nikos Dergiades' proof
  3. M. T. Naraniengar's proof
  4. An Unexpected Variant
  5. Proof by B. Stonebridge and B. Millar
  6. Proof by B. Stonebridge
  7. Proof by Roger Smyth
  8. Proof by H. D. Grossman
  9. Proof by H. Shutrick
  10. Original Taylor and Marr's Proof of Morley's Theorem
  11. Taylor and Marr's Proof - R. A. Johnson's Version
  12. Morley's Theorem: Second Proof by Roger Smyth
  13. Proof by A. Robson

Algebraic proofs

  1. Morley's Redux and More, Alain Connes' proof

Invalid proofs

  1. Bankoff's conundrum
  2. Proof by Nolan L Aljaddou
  3. Morley's Theorem: A Proof That Needs Fixing

Related material
Read more...

  • Equilateral and 3-4-5 Triangles
  • Rusty Compass Construction of Equilateral Triangle
  • Equilateral Triangle on Parallel Lines
  • Equilateral Triangle on Parallel Lines II
  • When a Triangle is Equilateral?
  • Viviani's Theorem
  • Viviani's Theorem (PWW)
  • Tony Foster's Proof of Viviani's Theorem
  • Viviani in Isosceles Triangle
  • Viviani by Vectors
  • Slanted Viviani
  • Slanted Viviani, PWW
  • Morley's Miracle
  • Triangle Classification
  • Napoleon's Theorem
  • Sum of Squares in Equilateral Triangle
  • A Property of Equiangular Polygons
  • Fixed Point in Isosceles and Equilateral Triangles
  • Parallels through the Vertices of Equilateral Triangle

    • |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    71074117