Equilateral and 3-4-5 Triangles
In an equilateral triangle ABC a point P is found such that
29 April 2015, Created with GeoGebra
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
In an equilateral triangle ABC a point P is found such that
The problem resembles one in a square, where a point was joined to three vertices of the square with segments of lengths 3, 4, and 5. In addition, there had to be significance to the lengths being the sides of the 3-4-5 triangle. The applet below illustrates the solution.
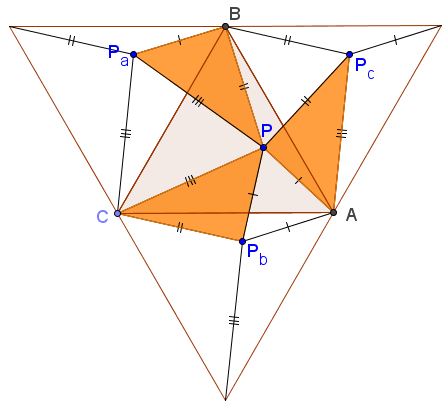
Rotate ΔABC 60° around each of its vertices, all in the same direction. This will produce and equilateral triangle consisting of 4 copies of ΔABC, with three images of point P: Pa, Pb, Pc. The area of hexagon APcBPaCPb can be evaluated in two ways.
First, note that the complement of the hexagon in the big triangle consists of copies of triangles ABP, BCP, and CAP, each appearing twice. It follows that
Also, the hexagon is the union of three equilateral triangles, with sides 3, 4, 5, and of three 3-4-5 triangles, which we know to be right by the converse of the Pythagorean theorem. We see that
2 Area(a) = Area(3) + Area(4) + Area(5) + 3×(3·4/2),
where Area(x) denotes the area of an equilateral triangle with side x and a is the unknown side of ΔABC. Since
A(x) = x²√3/4,
we are led to the following equation:
2 a²√3/4 = (3² + 4² + 5²)√3/4 + 18,
solving which we find that
a² = (25 √3/4 + 9) 4 / √3.
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73563815
