Slanted Viviani, PWW

What Might This Be About?

Problem

$ABC$ is an equilateral triangle. Cevians $AD,$ $BE,$ $CF$ are equal (and, for the esthetics' sake, equally inclined to the corresponding sides.) Points $M,N,P$ are on $BC,AC,AB,$ respectively, such that $OM\parallel AD,$ $ON\parallel BE,$ and $OP\parallel CF.$

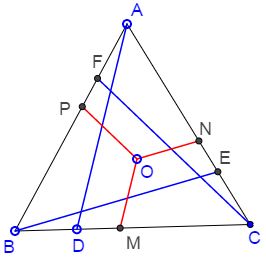
Slanted Viviani, problem

Prove that $OM+ON+OP=AD.$

Proof

The proof is supposed to be self-explanatory.

Slanted Viviani, PWW

In case of difficulties in interpretation, please, have a look at a more explicit variant.

Acknowledgment

The illustration is by Grégoire Nicollier.

Related material
Read more...

  • Equilateral and 3-4-5 Triangles
  • Rusty Compass Construction of Equilateral Triangle
  • Equilateral Triangle on Parallel Lines
  • Equilateral Triangle on Parallel Lines II
  • When a Triangle is Equilateral?
  • Viviani's Theorem
  • Viviani's Theorem (PWW)
  • Tony Foster's Proof of Viviani's Theorem
  • Viviani in Isosceles Triangle
  • Viviani by Vectors
  • Slanted Viviani
  • Morley's Miracle
  • Triangle Classification
  • Napoleon's Theorem
  • Sum of Squares in Equilateral Triangle
  • A Property of Equiangular Polygons
  • Fixed Point in Isosceles and Equilateral Triangles
  • Parallels through the Vertices of Equilateral Triangle

    • |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    71536013