Equilateral Triangle on Parallel Lines II
Construct an equilateral triangle whose vertices lie on three parallel lines (one vertex per line.)
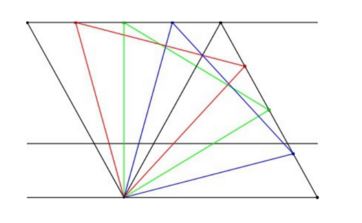
In the applet below, each of the parallel lines can be dragged up or down. One one of the lines there is a draggable point that serves as a common vertex of two equilateral triangles, that share on side and have bases on two of the parallel lines. There is another draggable point, opposite the common moving vertex. This, too, serves as a vertex of an equilateral triangle. What can be said about the third vertex of that triangle as the second one glides along the line it is on?
10 February 2016, Created with GeoGebra
|Activities| |Contact| |Front page| |Contents| |Geometry| |Eye opener|
Copyright © 1996-2018 Alexander Bogomolny
Construct an equilateral triangle whose vertices lie on three parallel lines (one vertex per line.)
The solution that can be found in D. Wells book Motivating mathematics illustrates an application of the Fundamental Theorem of Directly Similar Figures.
Given three parallel lines $p,q,r,\;$ it is a simple matter to construct two equilateral triangles $FHP\;$ and $HKP.\;$ $F,H\;$ on $r,\;$ $P,K\;$ on $P.$
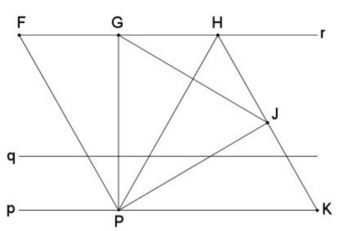
This may be an unexpected observation that for a point $G\;$ on $r\;$ the third vertex $J\;$ of the equilateral triangle $PGJ\;$ lies on the line $HK.\;$
This leads to an immediate solution the posed problem: take $J\;$ as the intersection of $HK\;$ with $q\;$ - the third of the parallel lines. $G\;$ then can be found at the intersection of the perpendicular bisector of $JP\;$ and $r\;$ such that the triangle $GJP\;$ is equilateral.
(A different construction can be found elsewhere. Also, the problem extends to the case where the three lines are in general position, i.e., not necessarily parallel.)
References
- D. Wells, Motivating Mathematics, Imperial College Press (December 15, 2015), 76-85
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73614991
