Morley's Miracle
J. Arioni's Proof
John Arioni
May 27, 2017
Let's take an arbitrary $\Delta ABC\,$ and trisect the angles $\alpha,\,$ $\beta,\,$ $\gamma\,$ of $\Delta ABC.\,$ (fig. 1)
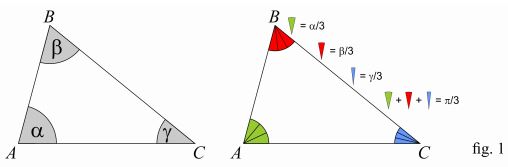
Let's construct three triangles, each around one copy of the same equilateral triangle as shown in fig. 2. The red, blue and green angles are the same angles $\alpha/3,\,$ $\beta/3,\,$ $\gamma/3\,$ of fig. 1.
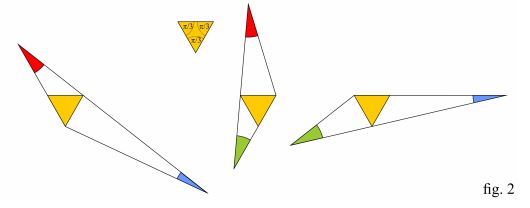
Rearranging the triangles of fig.2 by superimposing the equilateral triangles yields the six-pointed star of fig.3 here below:

Inside the six-pointed star there are represented six angles, highlighted with different shades of grey: these angles will play a key role in the problem. Equal shades of grey are used here to point out the pairs of angles that are congruent (as we'll see further on).
The triangles of fig. 2 will help us to evaluate such angles simply applying the rule of the sum of angles in some triangle.
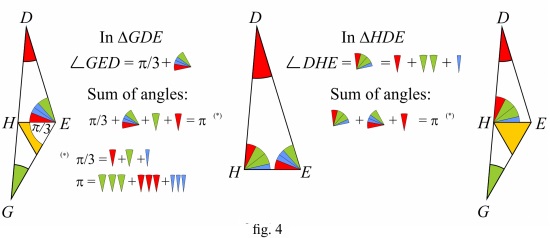
Fig.4 below provides an example applied to one of the triangles of fig.2. In red, blue and green are respectively angles $\alpha/3,\,$ $\beta/3,\,$ $\gamma/3\,$ of fig. 1.
Sum of angles of a triangle equals $\pi.$
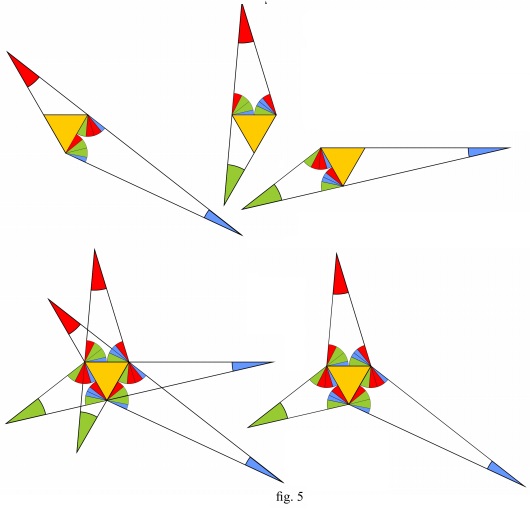
Repeating the same steps as in fig. 4 with the other two triangles of fig. 2, what we eventually get is represented, in fig. 5. The three-pointed star (fig.5 bottom right) is what is left of the six-pointed after removing the parts we don't need any longer.
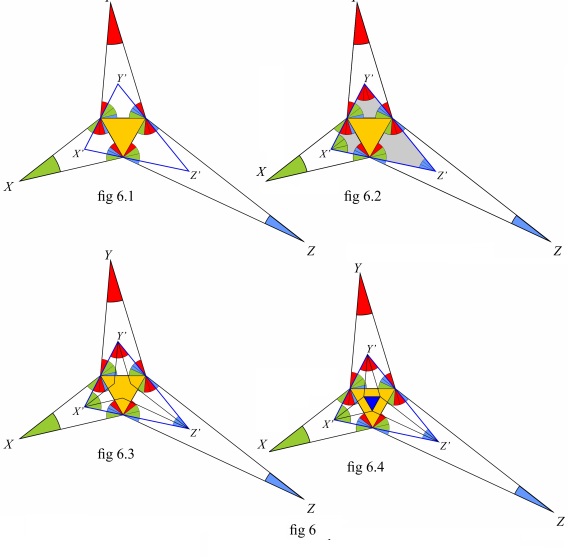
Inside the three-pointed star of fig. 5 let's construct the $\Delta X'Y'Z'\,$ as shown in fig. 6.1 (the triangle with blue sides).Then let's complete $\Delta X'Y'Z'\,$ with the vertex angles, simply applying the sum of angles rule to the three grey triangles of fig. 6.2 - it's plain that $\Delta X'Y'Z'\,$ and $\Delta ABC\,$ of fig. 1 are similar. Now let's construct (fig. 6.3) the three-pointed star $X'Y'Z';\,$ the three-pointed stars $X'Y'Z'\,$ and $XYZ\,$ have parallel sides (*) as well as congruent vertex angles, so they are similar.
Finally let's construct the blue triangle as in fig 6.4: it's plain that the blue and and yellow triangles are similar, then the blue triangle is equilateral, which proves Morley's theorem.
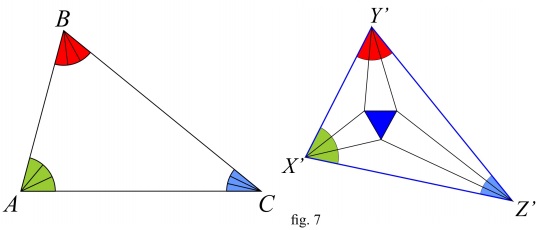
$\Delta ABC\,$ compared with $\Delta X'Y'Z':$
Morley's Miracle
On Morley and his theorem
- Doodling and Miracles
- Morley's Pursuit of Incidence
- Lines, Circles and Beyond
- On Motivation and Understanding
- Of Looking and Seeing
Backward proofs
- J.Conway's proof
- D. J. Newman's proof
- B. Bollobás' proof
- G. Zsolt Kiss' proof
- Backward Proof by B. Stonebridge
- Morley's Equilaterals, Spiridon A. Kuruklis' proof
- J. Arioni's Proof of Morley's Theorem
Trigonometric proofs
- Bankoff's proof
- B. Bollobás' trigonometric proof
- Proof by R. J. Webster
- A Vector-based Proof of Morley's Trisector Theorem
- L. Giugiuc's Proof of Morley's Theorem
- Dijkstra's Proof of Morley's Theorem
Synthetic proofs
- Another proof
- Nikos Dergiades' proof
- M. T. Naraniengar's proof
- An Unexpected Variant
- Proof by B. Stonebridge and B. Millar
- Proof by B. Stonebridge
- Proof by Roger Smyth
- Proof by H. D. Grossman
- Proof by H. Shutrick
- Original Taylor and Marr's Proof of Morley's Theorem
- Taylor and Marr's Proof - R. A. Johnson's Version
- Morley's Theorem: Second Proof by Roger Smyth
- Proof by A. Robson
Algebraic proofs
Invalid proofs
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73606089
