Parallels through the Vertices of Equilateral Triangle
Problem
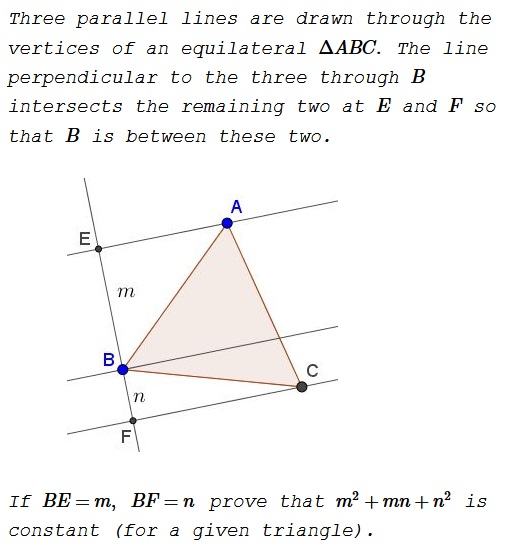
Solution 1
Let the angles be denoted as shown below:

Then, letting the side of the triangle be $1,$ $m=\cos\alpha$ and $n=\cos (120^{\circ}-\alpha).$ The problem reduces to showing that the expression
$X=\cos^2\alpha+\cos\alpha\cdot\cos (120^{\circ}-\alpha)+\cos^2(120^{\circ}-\alpha)$
is independent of $\alpha.\,$ This is indeed so. Since $\displaystyle \cos (120^{\circ}-\alpha)=-\frac{1}{2}\cos\alpha+\frac{\sqrt{3}}{2}\sin\alpha,$
$\displaystyle \begin{align} X&=\cos^2\alpha-\frac{1}{2}\cos^2\alpha+\frac{\sqrt{3}}{2}\cos\alpha\sin\alpha+\frac{1}{4}(\cos\alpha-\sqrt{3}\sin\alpha)^2\\ &=\frac{3}{4}\cos^2\alpha+\frac{3}{4}\sin^2\alpha=\frac{3}{4}. \end{align}$
Solution 2
Let $l$ be the side of the triangle. Then, for some angle $\phi$, $m=l\cos(60^o-\phi)$ and $n=l\cos(60^o+\phi)$.
$\displaystyle \begin{align} &m^2+mn+n^2=(m+n)^2-mn \\ &=l^2\left\{\left[\cos(60^o-\phi)+\cos(60^o+\phi)\right]^2-\cos(60^o-\phi)\cos(60^o+\phi)\right\}\\ &=l^2\left[4\cos^2 60^o\cos^2\phi-\frac{\cos 120^o}{2}-\frac{\cos 2\phi}{2}\right] \\ &=l^2\left[\cos^2\phi-\frac{\cos 120^o}{2}-\cos^2\phi+\frac{1}{2}\right]=\frac{3l^2}{4}. \end{align}$
Solution 3
Let $G$ be the intersection of the line through $B\,$ with $AC.\,$ If $l$ is the side length of the equilateral triangle, then $\displaystyle AG=\frac{lm}{m+n}\,$ and $\displaystyle CG=\frac{ln}{m+n}.\,$ Let $p$ be the length of $BG.$
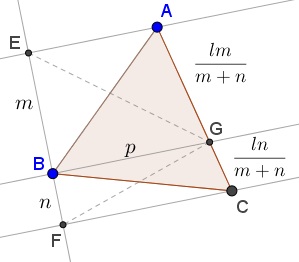
By Stewart's theorem in $\Delta ABC,\,$
$\displaystyle AB^2\cdot CG+BC^2\cdot AG-BG^2\cdot AC=AC\cdot AG\cdot CG,$
i.e., $\displaystyle l^2\cdot\frac{ln}{m+n}+l^2\frac{lm}{m+n}-p^2\cdot l=l\cdot\frac{lm}{m+n}\cdot\frac{ln}{m+n},\,$ from which $\displaystyle p^2=l^2\left(1-\frac{mn}{(m+n)^2}\right),\,$ or else
$p^2(m+n)^2=l^2(m^2+mn+n^2).$
Thus to prove that $m^2+mn+n^2$ is constant, suffice it to show tht $p(m+n)$ is constant. But $p(m+n)$ equals twice the area of $\Delta EFG.$ We'll show that $[\Delta EFG]=[\Delta ABC]$ so that the former is indeed constant.
Since triangles $BEG$ and $BAG$ share base $BG$ and have equal altitudes, $[\Delta BEG]=[\Delta BAG],$ by Euclid I.37. Similarly, $[\Delta BCG]=[\Delta BFG].\,$ Adding up, proves that $[\Delta EFG]=[\Delta ABC].$
Solution 4
We'll use complex coordinates, with the $x-\text{axis}$ passing through $C\,$ and the $y-\text{axis}$ through $B.$ Then $C=(x,0),\,$ $B=(0,n),\,$ $A=(y,m+n),\,$ i.e., $c=x+i\cdot 0,\,$ $b=0+i\cdot n,\,$ $a=y+i\cdot (m+n),\,$ $x,y\in\mathbb{R}.$
The fact that $AB$ is obtaind from $CB$ with a rotation through $\displaystyle \frac{\pi}{3}$ around $B$ is expressed as $\displaystyle (a-b)=(c-b)\left(\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}\right),$ or
$\displaystyle y+im+in-in=(x-in)\left(\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}\right)=(x-in)\left(\frac{1}{2}+i\frac{\sqrt{3}}{2}\right).$
In other words, $y+im=\frac{1}{2}x+\frac{\sqrt{3}}{2}n=i\left(\frac{\sqrt{3}}{2}x-\frac{1}{2}n\right)$ from which
(1)
$\displaystyle y=\frac{1}{2}x+\frac{\sqrt{3}}{2}n\,$ and $\displaystyle m=\frac{\sqrt{3}}{2}x-\frac{1}{2}n.$
(2)
$AB=CB=constant =|y+im|=\sqrt{y^2+m^2}.$
Thus, $\displaystyle m+\frac{n}{2}=\frac{\sqrt{3}}{2}x,\,$ so that $\displaystyle x=\frac{2m+n}{\sqrt{3}}\,$ and $\displaystyle y=\frac{m+2n}{\sqrt{3}}.$ Using these,
$\displaystyle \begin{align} |AB|^2&=y^2+m^2=\frac{(m+2n)^2}{3}+m^2=\frac{m^2+4mn+4n^2+3m^2}{3}\\ &=\frac{4}{3}(m^2+mn+n^2). \end{align}$
Finally, $\displaystyle m^2+mn+n^2=\frac{3}{4}AB^2=constant.$
Acknowledgment
The problem has been posted by Antreas Hatzipolakis as Problem 1179 at the Οι Ρομαντικοι της Γεωμετριας (Romantics of Geometry) facebook group. Solution 2 is by Amit Itagi; Solution 3 is by Mike Lawler; Solution 4 is by Marian Dinca.
A related problem of constructing an equilateral triangle with vertices on three parallel lines is discussed elsewhere.
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73562230
