Viviani's Theorem: What is it?
|
| Buy this applet What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2012 Alexander BogomolnyViviani's Theorem
The applet attempts to illustrate the following theorem:
The sum of distances of a point inside an equilateral triangle or on one of its sides equals the length of its altitude.
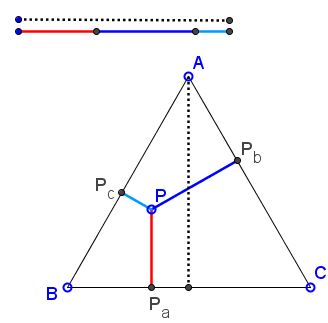
The theorem is named after Vincenzo Viviani (1622-1703).
| Buy this applet What if applet does not run? |
Let Pa, Pb, and Pc be the pedal points (projections) of a point P on the side lines BC, AC, and AB of ΔABC. Then the theorem claims that
| (1) | h = PPa + PPb + PPc, |
where h is the length of the altitudes of ΔABC.
To see that this is indeed so, draw the lines through P parallel to the sides of the triangle. I must mention that the current page has been prompted by a recent proof without words by Ken-ichiroh Kawasaki. The diagram below is just a slight modification of Kawasaki's proof:
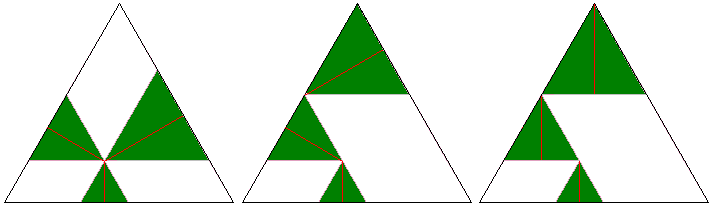
Together with the side lines of the base triangle, the newly drawn lines form three equilateral triangles, which, between them, contain all the pieces in (1) as their altitudes. A one step rearrangement of the triangles followed by a rotation of two of them completes this delightful proof.
The applet above was originally intended to present a dynamic variant of Kawasaki's proof. It ended up as something a little different, hopefully still simple enough:
| PPa + PPb + PPc | = TS + LU + LT |
| = VL + LU + TS | |
| = VS | |
| = h | |
One can arrive at the same conclusion without rotating the triangles:
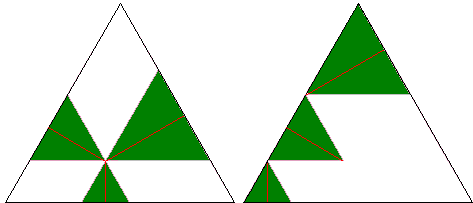
The sides of the three small equilateral triangle add up to the side of the big one. Hence, the same holds for their altitudes.
(There is available another proof without words of Viviani's theorem. For you to compare. Also, the theorem extends to equilateral as well as equiangular polygons.)
References
Proofs Without Words
- Proofs Without Words
- Sums of Geometric Series - Proofs Without Words
- Sine of the Sum Formula
- Parallelogram Law: A PWW
- Parallelogram Law
- Ceva's Theorem: Proof Without Words
- Viviani's Theorem
- A Property of Rhombi
- Triangular Numbers in a Square
- PWW: How Geometry Helps Algebra
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2012 Alexander Bogomolny| 40619350 |
