Morley's Theorem
Morley's theorem asserts that in the diagram below $\Delta XYZ$ is equilateral, whatever $\Delta ABC.$
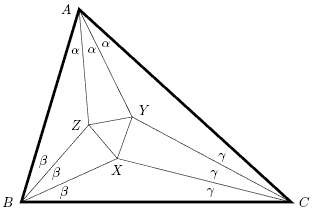
What follows has been communicated to me in private correspondence by Roger Smyth. Roger has based his new direct proof on the following
Lemma
Assume point $G$ in the interior of $\Delta DEF,$ with $\angle FED = 3\alpha,$ satisfies $\angle FEG=\alpha$ and $DE=EG.$
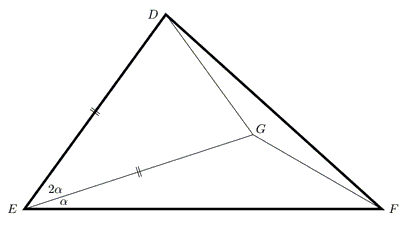
Then $DG=FG$ iff $\angle DFE$ equals $60^{\circ}-\alpha.$
Proof
Assume $DG=FG$ and let $H$ be the foot of the perpendicular from $G$ to $EF.$
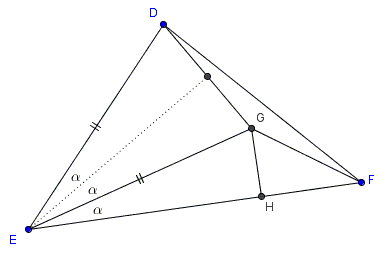
Since $GF = GD = 2GH$ it follows that $\angle GFE = 30^{\circ}.$ Thus, for the reflex $\angle DGF,$
$\begin{align} \angle DGF &= \angle DGE +\angle EGH + \angle FGH \\ &= 2(90^{\circ}-\alpha) + 60^{\circ} \\ &= 240^{\circ} -2\alpha. \end{align}$
Since we assumed $\Delta DGF$ isosceles, $\angle DFG =\angle FDG=30^{\circ}-\alpha;$ therefore, $\angle DFE=60^{\circ}-\alpha,$ as required.
Proof of Morley's Theorem
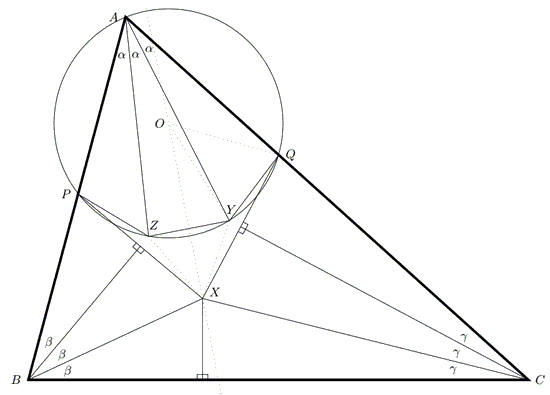
Above (as usual) $X$ is the Morley vertex adjacent to $BC$ and $P$ and $Q$ are the points on $AB$ and $AC$ such that $BP = BX$ and $CQ = CX.$ The circle through $A,$ $P,$ $Q$ is drawn and the angle trisectors from $A$ cut it at $Z$ and $Y.$ Thus the arcs $PZ,$ $ZY,$ $YQ$ are equal. Let the centre of the circle be $O.$ Since $\Delta XPQ$ is isosceles, the perpendicular bisector of $YZ$ goes through both $O$ and $X.$ Moreover, $\angle XOQ = 3\alpha$ and $\angle XOY = \alpha$ and $OY = OQ,$ so the conditions of the lemma are met in $\Delta QOX.$ $(Q \leftrightarrow D,$ $O \leftrightarrow E,$ $X \leftrightarrow F,$ $Y \leftrightarrow G).$
Now comes the crunch. The Morley point next to $A$C lies at the intersection of two trisectors, one of which is $AY$ and the other is also the perpendicular bisector of $QX.$ But $\angle QXO = \frac{1}{2}\angle QXP = 60^{\circ}-\alpha$ and, according to the lemma, this means that $QY=XY;$ thus the perpendicular bisector of $QX$ actually goes through $Y.$ So our search for the Morley point is over almost before it has begun! By symmetry $Z$ is the Morley vertex adjacent to $AB$ and $\Delta XYZ$ is equilateral because $PZ = ZX = XY = YQ = YZ.$
Morley's Miracle
On Morley and his theorem
- Doodling and Miracles
- Morley's Pursuit of Incidence
- Lines, Circles and Beyond
- On Motivation and Understanding
- Of Looking and Seeing
Backward proofs
- J.Conway's proof
- D. J. Newman's proof
- B. Bollobás' proof
- G. Zsolt Kiss' proof
- Backward Proof by B. Stonebridge
- Morley's Equilaterals, Spiridon A. Kuruklis' proof
- J. Arioni's Proof of Morley's Theorem
Trigonometric proofs
- Bankoff's proof
- B. Bollobás' trigonometric proof
- Proof by R. J. Webster
- A Vector-based Proof of Morley's Trisector Theorem
- L. Giugiuc's Proof of Morley's Theorem
- Dijkstra's Proof of Morley's Theorem
Synthetic proofs
- Another proof
- Nikos Dergiades' proof
- M. T. Naraniengar's proof
- An Unexpected Variant
- Proof by B. Stonebridge and B. Millar
- Proof by B. Stonebridge
- Proof by Roger Smyth
- Proof by H. D. Grossman
- Proof by H. Shutrick
- Original Taylor and Marr's Proof of Morley's Theorem
- Taylor and Marr's Proof - R. A. Johnson's Version
- Morley's Theorem: Second Proof by Roger Smyth
- Proof by A. Robson
Algebraic proofs
Invalid proofs
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73573020
