Original Taylor and Marr's Proof of Morley's Theorem
What is this about?
Problem
If the trisectors of the angles of a triangle are drawn so that those adjacent to each side intersect, the intersections are vertices of an equilateral triangle.
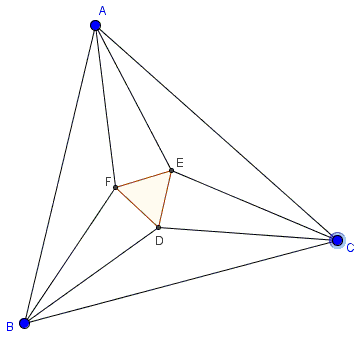
Hint
Morley's theorem or, as it is often referred to, Morley's Miracle has a long history and multiple proofs, many - if not all of which - have been documented at this site. Each of the proofs (and one that follows is no exception) sheds an extra light on Morley's wonderful discovery. Anyone who has an ambition to add to the collection, should exercise his or her ingenuity. Good luck and enjoy.
Solution
Let $\alpha,$ $\beta,$ $\gamma$ stand for $\displaystyle\frac{A}{3},$ $\displaystyle\frac{B}{3},$ $\displaystyle\frac{C}{3},$ respectively, so that $\displaystyle\alpha +\beta +\gamma=\frac{\pi}{3}.$ The pairs of trisectors of $B$ and $C$ meet in $D$ and $L.$ Draw the incircle of $\Delta LBC,$ center $D.$ Let $H,$ $K$ be the images of $D$ in $BL$ and $CL$. Draw the tangent $KP$ and produce to meet $BL$ in $F;$ $Q$ is the point of contact of $BL.$
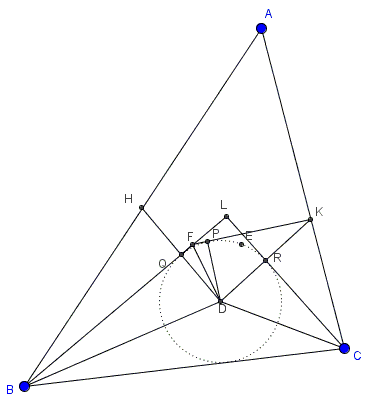
Since $\displaystyle DP=\frac{1}{2}DK,$ $\displaystyle\angle PKD=\frac{\pi}{6}$ and $\displaystyle\angle PDK=\frac{\pi}{3},$ $\displaystyle\angle QDR=\pi - L=2\beta +2\gamma=\frac{2\pi}{3}-2\alpha.$ It follows that
\( \begin{align}\displaystyle \angle FHQ=\angle FDQ=\frac{1}{2}\angle QDP &= \frac{1}{2}(\angle QDR-\frac{\pi}{3}) \\ &= \frac{\pi}{6}-\alpha. \end{align} \)
Also $\displaystyle\angle DHK=\angle DKH=\frac{1}{2}\angle L=\frac{\pi}{6}+\alpha,$ whence $\angle FHK=2\alpha,$ $\angle FKH=\alpha.$
Hence $\angle HFK=\pi -3\alpha =\pi - A,$ and $AHFK$ cyclic. It follows that $\angle HAF=\angle HKF=\alpha,$ and $AF$ is a trisector of $A.$ Similarly for $E,$ the meet of $CL$ and the tangent from $H.$
From the symmetry of the figure $DHK$ with respect to the circle it follows that $DF=DE$ and $\angle FDE$ is easily seen to be $\displaystyle\frac{\pi}{3}.$ Therefore, $\Delta DEF$ is equilateral.
Acknowledgment
This is the original proof as it appeared in the oft-quoted Taylor/Marr paper (Proceedings of Edinburgh Math. Society, 1914) which attributed it to W. E. Philip. I am grateful to Roger Smyth for bringing this proof to my attention.
The proof has appeared in Ross Honsberger's Mathematical Gems [p. 96-98] and in R. A. Johnson's Advanced Euclidean Geometry (Modern Geometry) [pp. 253-254], in the latter in a rather modified form which I reproduced in my earlier attempt, on seeing which Roger Smyth wrote to observe that the original proof is more transparent than that of Johnson's, in part because if Johnson's use of indices but also because of several elements drawn in the diagram that were not strictly necessary for the proof and thus cluttered the drawing. I think this is instructive to have both versions online to enable a curious reader easy comparison between the two.
Morley's Miracle
On Morley and his theorem
- Doodling and Miracles
- Morley's Pursuit of Incidence
- Lines, Circles and Beyond
- On Motivation and Understanding
- Of Looking and Seeing
Backward proofs
- J.Conway's proof
- D. J. Newman's proof
- B. Bollobás' proof
- G. Zsolt Kiss' proof
- Backward Proof by B. Stonebridge
- Morley's Equilaterals, Spiridon A. Kuruklis' proof
- J. Arioni's Proof of Morley's Theorem
Trigonometric proofs
- Bankoff's proof
- B. Bollobás' trigonometric proof
- Proof by R. J. Webster
- A Vector-based Proof of Morley's Trisector Theorem
- L. Giugiuc's Proof of Morley's Theorem
- Dijkstra's Proof of Morley's Theorem
Synthetic proofs
- Another proof
- Nikos Dergiades' proof
- M. T. Naraniengar's proof
- An Unexpected Variant
- Proof by B. Stonebridge and B. Millar
- Proof by B. Stonebridge
- Proof by Roger Smyth
- Proof by H. D. Grossman
- Proof by H. Shutrick
- Original Taylor and Marr's Proof
- Taylor and Marr's Proof - R. A. Johnson's Version
- Morley's Theorem: Second Proof by Roger Smyth
- Proof by A. Robson
Algebraic proofs
Invalid proofs
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73571251
