Morley's Miracle
R. J. Webster's Proof

Theorem

  The three points of intersection of the adjacent trisectors of the angles of any triangle form an equilateral triangle.

Proof

This proof appeared in Mathematics Magazine, Vol. 43, No. 4 (Sep., 1970), pp. 209-210.

Let ABC be a triangle with inradius r and circumradius R, and let the adjacent trisectors of angles A, B, C meet in A', B', C' as illustrated below. Morley's theorem states that ΔA'B'C' is equilateral. The proofs of this theorem, which are usually given, do not include calculation of the side of this triangle.

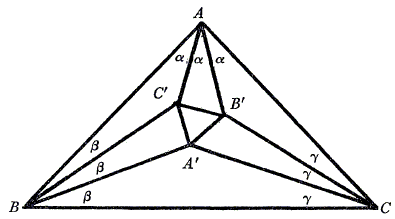
  Webster's proof of Morley's theorem, #1

In this note we prove Morley's theorem by showing that the side of this triangle is 8R sin(A/3)sin(B/3)sin(C/3). This is a particularly interesting result, when one recalls the formula r = 4R sin(A/2)sin(B/2)sin(C/2).

In any triangle ABC, we have a = 2R sin(A), etc. Let A = 3α, B = 3β, C = 3γ. Then applying the sine rule to A'BC we obtain

 A'B= 2R sin(3α) sinγ / sin(β + γ)
  = 2R (4sinα sin(60° + α) sin(60° - α) sinγ) / sin(60° - α)
  = 8R sinα sinγ sin(60° + α).
  Webster's proof of Morley's theorem, #2

Similarly, BC' = 8R sinα sinγ sin(60° + γ). Consider now triangle DEF shown above, where DE = 8R sinα sinγ sin(60° + α). It follows, using the sine rule on DEF, that EF = 8R sinα sinγ sin(60° + γ) and DF = 8R sinα sinβ sinγ. However, triangles A'BC' and DEF are congruent by SAS, so A'C' = DF = 8R sinα sinβ sinγ Thus, by the symmetry of the expression, the triangle A'B'C' is equilateral and Morley's theorem is proved.


Editorial Note: Professor C. N. Mills of Illinois State University at Normal as a tour de force found above expression for a side of the Morley triangle by a straightforward use of elementary Cartesian analysis! His complete proof required some twenty 8½×11 sheets of paper.


Morley's Miracle

On Morley and his theorem

  1. Doodling and Miracles
  2. Morley's Pursuit of Incidence
  3. Lines, Circles and Beyond
  4. On Motivation and Understanding
  5. Of Looking and Seeing

Backward proofs

  1. J.Conway's proof
  2. D. J. Newman's proof
  3. B. Bollobás' proof
  4. G. Zsolt Kiss' proof
  5. Backward Proof by B. Stonebridge
  6. Morley's Equilaterals, Spiridon A. Kuruklis' proof
  7. J. Arioni's Proof of Morley's Theorem

Trigonometric proofs

  1. Bankoff's proof
  2. B. Bollobás' trigonometric proof
  3. Proof by R. J. Webster
  4. A Vector-based Proof of Morley's Trisector Theorem
  5. L. Giugiuc's Proof of Morley's Theorem
  6. Dijkstra's Proof of Morley's Theorem

Synthetic proofs

  1. Another proof
  2. Nikos Dergiades' proof
  3. M. T. Naraniengar's proof
  4. An Unexpected Variant
  5. Proof by B. Stonebridge and B. Millar
  6. Proof by B. Stonebridge
  7. Proof by Roger Smyth
  8. Proof by H. D. Grossman
  9. Proof by H. Shutrick
  10. Original Taylor and Marr's Proof of Morley's Theorem
  11. Taylor and Marr's Proof - R. A. Johnson's Version
  12. Morley's Theorem: Second Proof by Roger Smyth
  13. Proof by A. Robson

Algebraic proofs

  1. Morley's Redux and More, Alain Connes' proof

Invalid proofs

  1. Bankoff's conundrum
  2. Proof by Nolan L Aljaddou
  3. Morley's Theorem: A Proof That Needs Fixing

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

71878372