Morley's Miracle
Dijkstra's Proof
I lifted this proof from the site of E. W. Dijkstra Archives at the University of Texas at Austin.
An open letter to Ross Honsberger.
University of Waterloo.
30 December 1975
Dear Sir,
the other day I encountered your delightful booklet "Mathematical Gems". On account of Chapter 8, I concluded that you might be interested in the following proof of Morley's Theorem "The adjacent pairs of the trisectors of a triangle always meet at the vertices of an equilateral triangle."
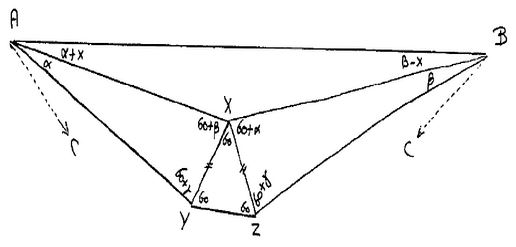
Choose $\alpha,$ $\beta$ & $\gamma \gt 0$ such that $\alpha + \beta + \gamma = 60^{\circ}.$ Draw an equilateral triangle $XYZ$ and construct the triangles $AXY$ and $BXZ$ with the angles as indicated. Because $\angle AXB = 180^{\circ} – (\alpha +\beta ),$ it follows that, if $\angle BAX = \alpha +x,$ $\angle ABX = \beta – x.$ Using the rule of sines three times (in $\Delta AXB,$ $\Delta AXY,$ and $\Delta BXZ),$ we deduce
$\begin{align}\displaystyle \frac{\sin (\alpha +x)}{\sin (\beta – x)}&=\frac{BX}{AX}\\ &=\frac{XZ\cdot\sin (60^{\circ}+\gamma)/\sin (\beta )}{XY\cdot\sin (60^{\circ}+\gamma)/\sin (\alpha )}\\ &=\frac{\sin (\alpha )}{\sin (\beta )}. \end{align}$
Because in the range considered, this equation has a left-hand-side which is a monotonically increasing function of $x$ (on account of the monotonicity of $\sin(\phi )$ in the first quadrant) we conclude $x = 0.$ Thus Morley’s Theorem is proved without any additional lines. I found this proof in the early sixties, but am afraid that I did not publish it. Yours ever,
Edsger W.Dijkstra
Morley's Miracle
On Morley and his theorem
- Doodling and Miracles
- Morley's Pursuit of Incidence
- Lines, Circles and Beyond
- On Motivation and Understanding
- Of Looking and Seeing
Backward proofs
- J.Conway's proof
- D. J. Newman's proof
- B. Bollobás' proof
- G. Zsolt Kiss' proof
- Backward Proof by B. Stonebridge
- Morley's Equilaterals, Spiridon A. Kuruklis' proof
- J. Arioni's Proof of Morley's Theorem
Trigonometric proofs
- Bankoff's proof
- B. Bollobás' trigonometric proof
- Proof by R. J. Webster
- A Vector-based Proof of Morley's Trisector Theorem
- L. Giugiuc's Proof of Morley's Theorem
- Dijkstra's Proof
Synthetic proofs
- Another proof
- Nikos Dergiades' proof
- M. T. Naraniengar's proof
- An Unexpected Variant
- Proof by B. Stonebridge and B. Millar
- Proof by B. Stonebridge
- Proof by Roger Smyth
- Proof by H. D. Grossman
- Proof by H. Shutrick
- Original Taylor and Marr's Proof of Morley's Theorem
- Taylor and Marr's Proof - R. A. Johnson's Version
- Morley's Theorem: Second Proof by Roger Smyth
- Proof by A. Robson
Algebraic proofs
Invalid proofs
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73609686
