G. Zsolt Kiss' proof from Interactive Mathematics Miscellany and Puzzles

Cut the knot: learn to enjoy mathematics

A math books store at a unique math study site. Shopping at the store helps maintain the site. Thank you.

Math & English enrichment at SchoolPlus-Online

Sites for teachers
Sites for parents
Terms of use
Awards
Interactive Activities

CTK Exchange
CTK Wiki Math
CTK Insights - a blog
Math Help

III Millennium Olympiad

Games & Puzzles
What Is What
Arithmetic/Algebra
Geometry
Probability
Outline Mathematics
Make an Identity
Book Reviews
Stories for Young
Eye Opener
Analog Gadgets
Inventor's Paradox
Did you know?...
Proofs
Math as Language
Things Impossible
Visual Illusions
My Logo
Math Poll
Cut The Knot!
MSET99 Talk
Other Math sites
Front Page
Movie shortcuts
Personal info
Privacy Policy

Guest book
News sites

Recommend this site

Games to relax

Sites for teachers
Sites for parents

Education & Parenting

Morley's Theorem
G. Zsolt Kiss' proof

This is the latest proof that was sent (September 02, 2006) to me by G. Kiss Zsolt from Hungary. Like Conway's and Newman's, this one, too, employs the cheating (backward) strategy. Also, one can't miss its relation to Conway's proof. It uses the same add-ons but in a more natural and symmetric manner.

Assume angles a, b, c are given such that a + b + c = 60^o. Pick up an equilateral triangle and, on its sides form isosceles trapezoids with base angles 2a, 2b, 2c, respectively, and the sides equal to the top base.

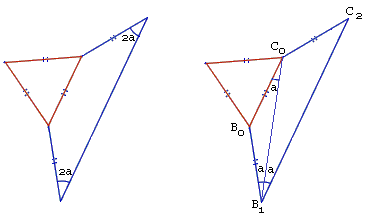
In such a trapezoid B₀B₁C₂C₀, the diagonals serve as the bisectors of the base angles. Indeed, assuming ∠B₀B₁C₂ = 2a, ∠B₁B₀C₀ = 180^o - 2a. And since, by construction, ΔB₁B₀C₀ is isosceles, its base angles equal

[180^o - (180^o - 2a)]/2 = a.

Now we form ΔABC by passing three straight lines through the dangling vertices of the trapezoids:

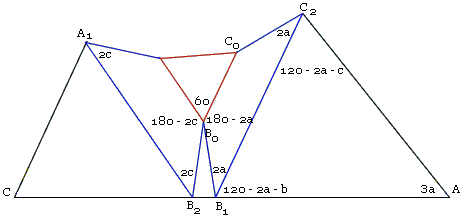
We get three small isosceles triangles, ΔB₀B₁B₂ is one of them. Its apex angle B₁B₀B₂ is found from

∠B₁B₀B₂	= 360^o - 60^o - (180^o - 2a) - (180^o - 2c)
	= 2a + 2c - 60^o
	= 2(60^o - b) - 60^o
	= 60^o - 2b.

Hence its base angles equal

[180^o - (60^o - 2b)]/2 = 60^o + b,

while the supplementary angle B₀B₁A = 120^o - b. Similarly,

∠C₀C₂A = 120^o - c.

It follows that ∠C₀B₁A = 120^o - a - b so that the two sum up to 180^o:

∠C₀C₂A + ∠C₀B₁A = 180^o.

This means that quadrilateral AC₂C₀B₁ is cyclic. In the same manner, quadrilateral AC₀B₀B₁ is also cyclic. Hence so is the pentagon AC₂C₀B₀B₁. Since, in the circumcircle, the three chords B₀B₁, B₀C₀, and C₀C₂ are equal, lines AB₀ and AC₀ trisect angle at A, which, as easily seen is 3a.

Now trying to reverse the steps, assume in ΔA'B'C' angles equal 3a, 3b, 3c so that a + b + c = 60^o. Starting with any equilateral triangle and following the above construction, we obtain ΔABC similar to ΔA'B'C'. Comparing the two we can modify the original equilateral triangle so as to obtain ΔABC equal to the given ΔA'B'C'. Which shows that the equilateral triangle is indeed obtained by Morley's trisectors.

Compared to Conway's or Newman's, it may be just a little longer but does not come even close to using trigonometry.

Hubert Shutrick sent me the following comment:

The third diagram in the proof shows how the vertices of ΔABC can be constructed using the points A₁, A₂, B₁, B₂, C₁, C₂ although A₂ and C₁ are not shown. Here is another motivation for these six points. Note that it is a straight edge and compass construction. Given the equilateral triangle A₀B₀C₀, the required vertex A has to be such that the angle B₀AC₀ is a and the locus of points making this angle is the arc of a circle through B₀ and C₀. Any other chord of the same length will also subtend the angle a for points on the circle. That is why B₁ is an interesting point. The angle B₀B₁C₀ is a so B₁ is on the circle and, since the length B₀B₁ is 1, the angle B₀AB₁ will be a for points A on the circular arc. Hence, if the theorem is true, B₁ must be on the side AC of the required triangle.

By symmetry, the six points mentioned above must be on the sides of the triangle ABC. The proof then consists of showing that it's angles are indeed 3a, 3b and 3c, simple angle calculations. There are two special cases that should be mentioned. There is the case a = b = c = 20�, when the theorem is obvious. The other case is when two of a, b, c add up to 40� without being equal. In this case, two of the six points coincide but the other four are distinct so the triangle ABC can still be constructed from them.

I found this proof long ago, in the 1970s, while teaching Euclidean geometry to prospective mathematics' teachers at Karlstad's university college.

Amic has observed that a correction is in order:

I read

"There are two special cases that should be mentioned. There is the case a = b = c = 20°, when the theorem is obvious. The other case is when two of a, b, c add up to 40° without being equal. In this case, two of the six points coincide but the other four are distinct so the triangle ABC can still be constructed from them."

There is a mistake : the other case is when a or b or c = 30°, and in fact we cannot define the line joining two points which are the same...

And I don't see why the case a = b = c = 20° is a special case...

So in my opinion this proof is wrong for a triangle ABC with a right angle.

My comment is that the proof can be saved by drawing the necessary line not "through two points" but at a certain angle at the "double point". For example, if b = 30° then B₁ and B₂ coincide and AC should be drawn as to form angles 90° - 2a and 90° - 2c with B₁C₂ and, respectively, B₂A₁.

Hubert Shutrick has later added the following:

If B' is the midpoint of B₁B₂, then B₀B' is orthogonal to AC and ∠C₀B₀B' is 150° + c - a since it is the mean of 180° - 2a and 360° - 60° - (180° - 2c). Similarly, ∠B₀C₀C' is 150° + b - a and the third exterior angle of the triangle formed by B₀B', C₀C' and B₀C₀ is indeed 3a. As for the special case that I bungled, if B₁ = B₂ = B', the calculation ensures that AC is the line orthogonal to B₀B'.

Morley's Miracle

33061195

Amazon.com Widgets

Morley's TheoremG. Zsolt Kiss' proof

Morley's Miracle

Morley's Theorem
G. Zsolt Kiss' proof