According to Steven Schwartzman, the word theorem originates with Greek theorema, theorein "to look at." Theater is a related borrowing, since "looking at" a play is what one does in a theater. And further: "A theorem was originally a sight or the act of seeing. Something that is looked at for any moment of time becomes an object of study. In mathematics, after studying a situation or a class of objects, a person hopes to make speculations and then prove them, so theorem came to mean the proof of a speculation that has been arrived at by looking at something." Theater, needless to say, came to mean something altogether different.

Mathematics - the only place where theorems live - and theater make an odd couple. There is nothing more alien to a visit to the theater than making speculations and then proving them. There is nothing less compatible with a mathematician's attitude than passive watching.

Just a few weeks ago, I took my little boy to a stage rendering of Eric Carle's The Very Hungry Caterpillar and The Very Quiet Cricket. It was all very nice until after the cricket found its soul mate and began chirping away its love song. The lights went on, and the two puppeteers took turns explaining how things worked and the purpose of the black background and clothes. The boy, who followed in awe the adventures of the caterpillar and the cricket, showed little interest in the sequel. The public streamed to the exits even as the puppeteers were demonstrating their tricks in controlling the insects with long sticks.

The Magician's Code precludes revealing the workings of a magic trick to a non-magician. There ought to be a similar puppeteers' convention. In theater, the audience is being entertained. Spectators live through a story and experience amazement. Rationalization is hardly consistent with the sensory involvement.

It's different in mathematics, in part because, in mathematics, looking has a different purpose. The desire to grasp and explain -- to figure it out -- is the driving force behind the mathematician's attitude. Even in the simplest cases of proofs without words, mathematician uses the mind's eye to see what's out there. Seeing in mathematics and having figured it out is mostly one and the same. Or, as a corollary from the Strong Law of Small Numbers has it, You can't tell by looking [Guy].

This, of course, is not to say that there's no entertainment or amazement in mathematics. The opposite is true. It's just that one can't buy a ticket to an entertaining math performance. To one extent or another one must be an actor in the play, not a passive spectator.

Ceva's theorem might have been discovered by looking, but was not until late in the 17^th century. Frank Morley did not draw the diagrams at all (see [Oakley] and Clark Kimberling's account). So Morley's theorem was not discovered by looking either, and I do not believe it might have been. It's most spectacular nonetheless.

It was observed much later [Sastry] that Morley's configuration is a rich source of numerous concurrences, which I am sure F. Morley has plainly overlooked. The reason I think so is that Morley's theorem is merely a by-product of Morley's investigation into a hierarchy of constructions generalizing the Clifford chain. His goal was to develop a theory, not study disparate examples.

More concurrences were suggested quite recently by L. Cusick and Antreas P. Hatzipolakis. They are not as curious as Morley's theorem itself and nowhere as useful as Ceva's. Their main source of attraction is in their quantity and in the fact that some are in fact only near hits (or is it near misses?), appearances notwithstanding.

Morley discovered 27 equilateral triangles formed by three families of three parallel lines each. The number of possible concurrences in the diagram is quite overwhelming. To keep the total to a manageable size, the applet below only incorporates two of Morley's triangles. One is formed at the intersections of adjacent internal trisectors (PQR in the diagram below), the other by their external counterparts (not shown, P'Q'R' in what follows)

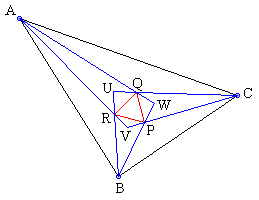
The lines PP', QQ', RR' are concurrent. Put differently, triangles PQR and P'Q'R' are perspective. Following is a complete list of triangles available in the applet below that may be (occasionally) mated into perspective pairs.

ABC		is the basic triangle whose vertices are draggable
PQR		Morley's first triangle
P'Q'R'		Morley's second triangle
UVW		triangle obtained at the intersection of not adjacent trisectors
U'V'W'		similar to UVW, but formed by the external trisectors
LLL (ABC-PQR)		Formed by points of intersection of angle bisectors of ΔABC with the corresponding sides of ΔPQR
LLL (PQR-ABC)		Formed by points of intersection of angle bisectors of ΔPQR with the corresponding sides of ΔABC
LLL (AQC-AC)		Formed by points of intersection of the bisectors of angles AQC, CPB, and BRA with sides AC, CB, and BA of ΔABC
AAA (ABC-PQR)		Formed by points of intersection of perpendiculars from vertices ABC to the corresponding sides of ΔPQR
AAA (PQR-ABC)		Formed by points of intersection of perpendiculars from vertices PQR to the corresponding sides of ΔABC
LLL (ABC-P'Q'R')		Formed by points of intersection of angle bisectors of ΔABC with the corresponding sides of ΔP'Q'R'
LLL (P'Q'R'-ABC)		Formed by points of intersection of angle bisectors of ΔP'Q'R' with the corresponding sides of ΔABC
LLL (AQ'C-AC)		Formed by points of intersection of the bisectors of angles AQ'C, CP'B, and BR'A with sides AC, CB, and BA of ΔABC
AAA (ABC-P'Q'R')		Formed by points of intersection of perpendiculars from vertices ABC to the corresponding sides of ΔP'Q'R'
AAA (P'Q'R'-ABC)		Formed by points of intersection of perpendiculars from vertices P'Q'R' to the corresponding sides of ΔABC
III (QAR)		Formed by the incenters of triangles QAR, RBP, PCQ
III (ABR)		Formed by the incenters of triangles ABR, BCP, CAQ
OOO (QAR)		Formed by the circumcenters of triangles QAR, RBP, PCQ
OOO (ABR)		Formed by the circumcenters of triangles ABR, BCP, CAQ
III (Q'AR')		Formed by the incenters of triangles Q'AR', R'BP', P'CQ'
III (ABR')		Formed by the incenters of triangles ABR', BCP', CAQ'
OOO (Q'AR')		Formed by the circumcenters of triangles Q'AR', R'BP', P'CQ'
OOO (ABR')		Formed by the circumcenters of triangles ABR', BCP', CAQ'
HHH (QAR)		Formed by the orthocenters of triangles QAR, RBP, PCQ
HHH (ABR)		Formed by the orthocenters of triangles ABR, BCP, CAQ
HHH (Q'AR')		Formed by the orthocenters of triangles Q'AR', R'BP', P'CQ'
HHH (ABR')		Formed by the orthocenters of triangles ABR', BCP', CAQ'

In addition, the applet allows one to consider pairs of isogonal lines instead of two angle trisectors. This is achieved by clicking on the numerator and the denominator of the fraction at the bottom of the applet. Numbers increase/decrease if clicked on to the left/right of their central vertical lines. The number that may be displayed in the upper left corner of the applet is the area of the triangle formed by three straight lines whose concurrence is being investigated. The number, of course, is only approximate.

---

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

---

For example, let's establish a couple of concurrences. Our main tool will be Ceva's theorem. I shall assume angles A, B and C equal to 3a, 3b and 3g, respectively.

Triangles ABC and LLL (AQC-AC) are perspective

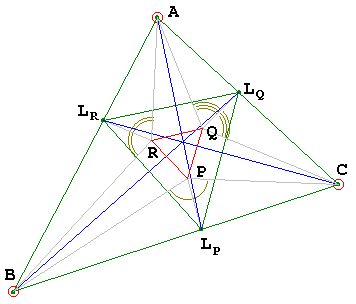
Indeed, let L_P, L_Q and L_R be the points of intersection of bisectors of angles CPB, AQC, and BRA with sides CB, AC and BA, respectively. We want to show that triangles ABC and L_PL_QL_R are perspective. Indeed, from the Law of Sines,

RL_R/sina = AL_R/sin(60° + g) and also RL_R/sinb = BL_R/sin(60° + g),

so that

sinb/sina = BL_R/AL_R,

and similarly for the other two sides. As the result, we get

BL_R/AL_R · AL_Q/CL_Q · CL_P/BL_P = 1,

which, by Ceva's theorem exactly means that the three lines are concurrent.

Triangles PQR and AAA (ABC-PQR) are perspective

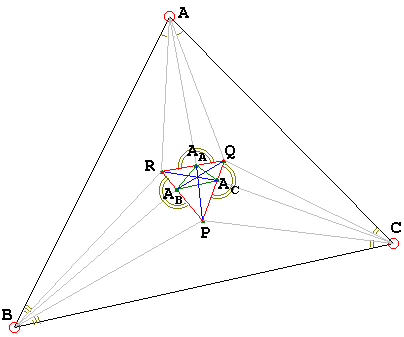
Let A_A, A_B, A_C be the feet of perpendiculars from A, B, and C to RQ, PR and PQ, respectively. We want to show that triangles PQR and A_AA_BA_C are perspective. Recall that ∠AQR = ∠BPR = g + 60°, ∠ARQ = ∠CPQ = b + 60° and ∠BRP = ∠CQP = a + 60°. It follows that

QA_A = AA_A·cot(g + 60°) and RA_A = AA_A·cot(a + 60°),

so that QA_A/RA_A = cot(g + 60°)/cot(a + 60°). Two additional ratios are found in a similar manner, and finally we get

QA_A/RA_A · RA_B/PA_B · PA_C/QA_C = 1,

which again, by Ceva's theorem, proves our claim.

Ceva's theorem could be used to establish a few more concurrences. Not all are as simple as the above. And probably Ceva's theorem is not the best way to approach the problem in all cases. E.g., Nikos Dergiades gave a very elegant proof that triangles OOO (ABR) and OOO (ABR) are perspective without invoking Ceva's theorem. However, following are two negative results proven with Ceva's theorem.

Triangles ABC and HHH (AQR) are not perspective (Antreas P. Hatzipolakis)

Let H_A, H_B and H_C denote the orthocenters of triangles AQR, BPR and CPQ, respectively. If the triangles ABC and H_AH_BH_C were perspective, the trigonometric form of Ceva's theorem would apply

sin(∠H_BBA)/sin(∠H_BBC) · sin(∠H_CCB)/sin(∠H_CCA) · sin(∠H_AAC)/sin(∠H_AAB) = 1

We'll show that the above is not necessarily true. Indeed,

∠HAAC	= ∠HAAQ + ∠QAC
	= (90° - ∠AQR) + ∠BAR
	= 90° - (60° + c) + a
	= 30° + (a - c).

Similarly H_AAB = 30° + (a - b), etc.

So, Ceva's identity becomes:

sin(30° + (b - a)) / sin(30° + (b - c)) · sin(30° + (c - b)) / sin(30° + (c - a)) · sin(30° + (a - c)) / sin(30° + (a - b)) = 1,

and is clearly not true in general.

Triangles III (ABR) and III (AQR) are not perspective (Milorad Stevanovic).

This is not a simple result. Its verification is left to full and part-time actors and active onlookers. There are many more like that to look for. Please let us know if you see any. We shall be looking forward to new insights.

References

1. L. Cusick, A Theorem concerning the Trisectors of a Triangle, geometry.research, Sun, 13 Sep 1998
2. R. Guy, The Strong Law of Small Numbers, in The Lighter Side of Mathematics, R. Guy and R. Woodrow (eds), MAA, 1994
3. C. O. Oakley and J. C. Baker, The Morley Trisector Theorem, Amer Math Monthly, 85 (1978) 737-745
4. K. R. S. Sastry, Constellation Morley, Math Mag 47 (1974) 15-22
5. S. Schwartzman, The Words of Mathematics, MAA, 1994

Morley's Miracle

On Morley and his theorem

1. Doodling and Miracles
2. Morley's Pursuit of Incidence
3. Lines, Circles and Beyond
4. On Motivation and Understanding
5. Of Looking and Seeing

Backward proofs

1. J.Conway's proof
   • Remarks on J. Conway's proof
2. D. J. Newman's proof
3. B. Bollobás' proof
4. G. Zsolt Kiss' proof
5. Backward Proof by B. Stonebridge
6. Morley's Equilaterals, Spiridon A. Kuruklis' proof
7. J. Arioni's Proof of Morley's Theorem

Trigonometric proofs

1. Bankoff's proof
2. B. Bollobás' trigonometric proof
3. Proof by R. J. Webster
4. A Vector-based Proof of Morley's Trisector Theorem
5. L. Giugiuc's Proof of Morley's Theorem
6. Dijkstra's Proof of Morley's Theorem

Synthetic proofs

1. Another proof
2. Nikos Dergiades' proof
3. M. T. Naraniengar's proof
4. An Unexpected Variant
5. Proof by B. Stonebridge and B. Millar
6. Proof by B. Stonebridge
7. Proof by Roger Smyth
8. Proof by H. D. Grossman
9. Proof by H. Shutrick
10. Original Taylor and Marr's Proof of Morley's Theorem
11. Taylor and Marr's Proof - R. A. Johnson's Version
12. Morley's Theorem: Second Proof by Roger Smyth
13. Proof by A. Robson

Algebraic proofs

1. Morley's Redux and More, Alain Connes' proof

Invalid proofs

1. Bankoff's conundrum
2. Proof by Nolan L Aljaddou
3. Morley's Theorem: A Proof That Needs Fixing

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny