Morley's Equilaterals, Spiridon A. Kuruklis' proof
What is this about?
Introduction
In what follows I outline Spiridon A. Kuruklis' extensive treatment of Morley's theorem.
Commonly, the appellation of "Morley's theorem" refers to the following
The three points of intersection of the adjacent trisectors of the angles of any triangle form an equilateral triangle.
This is probably the most striking consequences of F. Morley's results from 1899. A particular case of the latter, was a configuration of three triples of parallel lines inclined $60^{\circ}$ to each other, thus forming $27$ equilateral triangles. As Morley noticed at the time, one of the triangles was formed by the intersections of the trisectors of the (inner) angles of the given triangle, hence, Morley's theorem.
The earliest elementary treatment of Morley's theorem is due to F. Granville Taylor and W. L. Marr (1913). In addition to giving three elementary proofs of the theorem, they extended the theorem to the original Morley's by augmenting the angles at every vertex of a triangle by $2p\pi,$ $(p=0,1,2)$ and adding their trisectors. With the trisectors taken one per vertex and varying $p,$ there are $27$ equilateral and $9$ non equilateral triangles
The $27$ points lie six by six on $9$ straight lines, which are $3$ by $3$ parallel, and inclined at $60^{\circ}.$
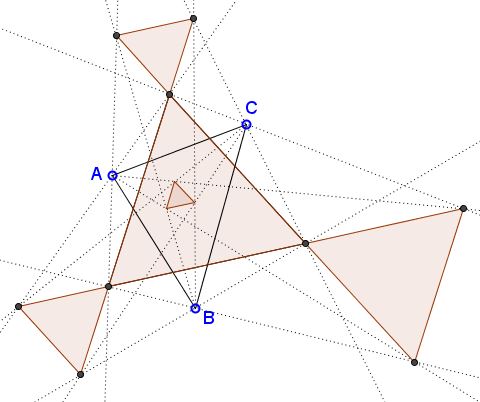
Since then the focus was on the unique triangle formed by the adjacent inner trisectors. Spiridon Kuruklis makes a break with the established tradition by considering the trisectors of the inner as well as exterior angles of a triangle. He finds that there are exactly five equilateral triangles among $64$ determined by the possible intersections of the trisectors (both of the inner and exterior angles of a triangle) taken one per vertex.
Spiridon's proofs are "backward", with the analysis showing the distribution of the angles between the trisectors and the allegedly equilateral triangles. Then in the synthesis part, he starts with an equilateral triangle and using the available angle information builds the a triangle with the given angles. In all the proofs the used is made of the following elegant lemma that allows determining the incenter (or excenter) of a given triangle with a single angle bisector:
Lemma
The incenter $I$ of $\Delta XYZ$ lies on a circular arc through $X$ and $Y$ whose angular measure equals $\displaystyle 90^{\circ}+\frac{\angle XZY}{2}.$
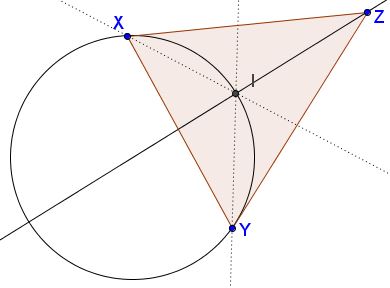
Spiridon refers to that statement as the Incenter Lemma. Naturally a similar result holds for the excircles of the triangle.
Proof of Morley's Theorem
Assuming the angles of $\Delta ABC$ measure $3\alpha,$ $3\beta,$ and $3\gamma,$ the analysis part of the proof has established the following distribution of the angles adjacent to the alleged equilateral triangle.
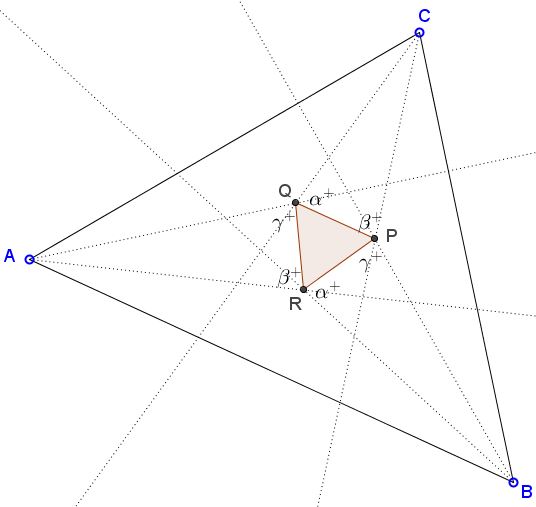
In the diagram $\alpha^{+}=\alpha+60^{\circ},$ $\beta^{+}=\beta+60^{\circ},$ $\gamma^{+}=\gamma+60^{\circ}.$ Going backwards, i.e., starting with an equilateral triangle $PQR,$ erect triangles $AQR,$ $BRP,$ and $CPQ.$ Introduce $R'$ - the intersection of $AQ$ and $BP.$
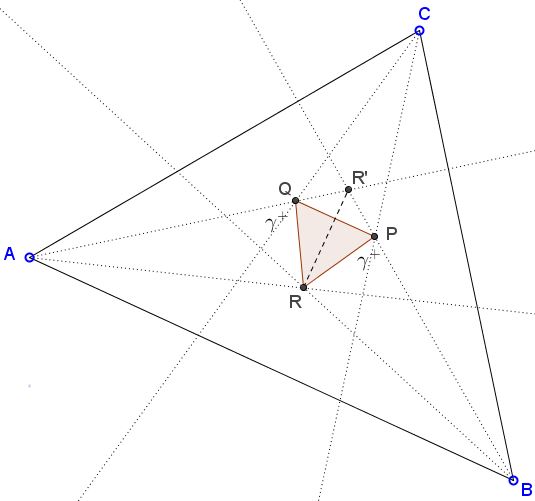
Observe that $\Delta PR'Q$ is isosceles as two of its angles are equal:
$\begin{align} \angle PQR'=\angle QPR' &= 180^{\circ}-60^{\circ}-(\gamma +60^{\circ})\\ &=60^{\circ}-\gamma. \end{align}$
Thus $\Delta RQR'=\Delta RPR'$ by SSS. It follows that $R$ lies on the bisector of $\angle PR'Q$ which is, by the way,
$\angle PR'Q=180^{\circ}-2(60^{\circ}-\gamma)=60^{\circ}+2\gamma.$
Since angle $AR'B$ is exactly the same as $\angle PR'Q,$ $AR'B=60^{\circ}+2\gamma.$ On the other hand,
$\begin{align}\displaystyle \angle ARB &= 360^{\circ}-60^{\circ}-\alpha^{+} -\beta^{+}\\ &=180^{\circ}-(\alpha +\beta) \\ &=120^{\circ}+\gamma\\ &=90^{\circ}+\frac{1}{2}(60^{\circ}+2\gamma)\\ &=90^{\circ}+\frac{1}{2}\angle AR'B. \end{align}$
It then follows by the Incenter Lemma, that $R$ is the incenter of $\Delta AR'B.$ Similarly, if $P'$ is the intersection of $BR$ and $CQ$ and $Q'$ that of $AR$ and $CP,$ then $P$ is the incenter of $\Delta BP'C,$ whereas $Q$ is the incenter of $\Delta AQ'C.$ So, for example,
$\angle ACQ =\angle QCP=\angle PCB,$
making $CP$ and $CQ$ the trisectors of $\angle ACB.$
Additional results
As was mentioned in the Introduction, Spiridon A. Kuruklis proves there are five equilateral triangles. How the other four are obtained? Spiridon notes that, relative to a side, an angle trisector (that naturally come in pairs) may be proximal or distal. For example, $CP$ is proximal to $BC$ but distal for $AC.$ (Spiridon introduces very clever and convenient notations that are useful in discussing all possible intersections of the inner and exterior trisectors. I can't give justice to the notations because I only cover the inner equlateral triangle.) Two trisectors at two vertices of a triangle may be both proximal, both distal, or mixed, relative to the side joining those vertices. The "standard" Morley triangle is formed by the intersections of proximal (inner) trisectors.
Four additional triangles are proved to be equilateral:
In any triangle the exterior trisectors of its angles, proximal to the sides, meet at the vertices of an equilateral (central Morley triangle.)
In any triangle the interior trisectors of an angle and the exterior trisectors of the other two angles, proximal the three sides respectively, meet at the vertices of an equilateral (three exterior Morley triangles.)
In proofs are to a great extent analogous from case to case, but not trivially so. I refer for the details to the earlier quoted paper. In the process, by observing the angles the sides of the equilaterals form with the trisectors, Spiridon shows that the sides of the five equilateral triangles are parallel.
Finally he observes that the configuration of the inner and three exterior Morley triangles is reminiscent of the configuration of the incenter and three excenters of a triangle and suggests that "trisectors behave like bisectors with equilaterals instead of points (which) invites further exploration. New results could be inspired from the vast variety of the angle bisectorsí point-line-circle theorems revealing more exciting analogies between the two structures."
Morley's Miracle
On Morley and his theorem
- Doodling and Miracles
- Morley's Pursuit of Incidence
- Lines, Circles and Beyond
- On Motivation and Understanding
- Of Looking and Seeing
Backward proofs
- J.Conway's proof
- D. J. Newman's proof
- B. Bollobás' proof
- G. Zsolt Kiss' proof
- Backward Proof by B. Stonebridge
- Morley's Equilaterals, Spiridon A. Kuruklis' proof
- J. Arioni's Proof of Morley's Theorem
Trigonometric proofs
- Bankoff's proof
- B. Bollobás' trigonometric proof
- Proof by R. J. Webster
- A Vector-based Proof of Morley's Trisector Theorem
- L. Giugiuc's Proof of Morley's Theorem
- Dijkstra's Proof of Morley's Theorem
Synthetic proofs
- Another proof
- Nikos Dergiades' proof
- M. T. Naraniengar's proof
- An Unexpected Variant
- Proof by B. Stonebridge and B. Millar
- Proof by B. Stonebridge
- Proof by Roger Smyth
- Proof by H. D. Grossman
- Proof by H. Shutrick
- Original Taylor and Marr's Proof of Morley's Theorem
- Taylor and Marr's Proof - R. A. Johnson's Version
- Morley's Theorem: Second Proof by Roger Smyth
- Proof by A. Robson
Algebraic proofs
Invalid proofs
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73609368
