Morley's Theorem: A Proof That Needs Fixing

Morley's theorem asserts that in the diagram below $\Delta A'B'C'$ is equilateral, whatever $\Delta ABC.$

The proof below is taken verbatim from a recent book on problem-solving.

Let $\angle BAC=3\alpha,$ $\angle ABC=3\beta,$ $\angle ACB=3\gamma.$ Let $B',$ $T,$ $S$ be the points of intersection of the trisectors.

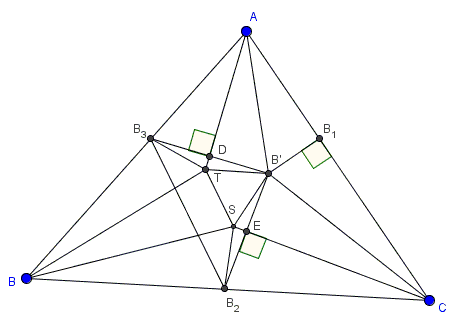
If we assume that $2\alpha +2\gamma\le 60^{\circ},$ $2\alpha +2\beta\le 60^{\circ},$ and $2\beta +2\gamma\le 60^{\circ}$ then

$4\alpha +4\beta+4\gamma\le 180^{\circ},$

i.e., $\alpha +\beta+\gamma\le 45^{\circ},$ which implies $3\alpha +3\beta+3\gamma\le 135^{\circ},$ or, equivalently, $180^{\circ}\le 135^{\circ},$ a contradiction. We conclude that one of the sums $2\alpha +2\gamma,$ $2\alpha +2\beta,$ $2\beta +2\gamma$ should exceed $60^{\circ}.$ Suppose $2\alpha +2\gamma\gt 60^{\circ},$ then $\angle ABC\lt 90^{\circ}.$

Let $B'B_{1}\perp AC$ and $B'B_{3}\perp AT.$ Then, since every point of the angle bisector is equidistant from both sides of the angle, we get

$B'B_{3}=2B'D=2B'B_{1}.$

Similarly, if we consider $B'B_{2}\perp CS,$ we obtain $B'B_{2}=2B'B_{1},$ and thus

$B'B_{2}=B'B_{3}.$

We also observe that $\angle B_3B'B_{2}=2\alpha+2\gamma\gt 60^{\circ}.$

Consider the points $A',$ $C'$ on the semi-straight lines $AT$ and $CS,$ respectively, so that triangle $A'B'C'$ is isosceles. We obviously have

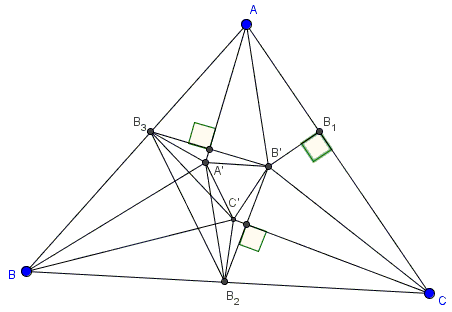
$\angle A'B'B_{3}=\angle C'B'B_{2}=s,$

therefore

$2s=2\alpha +2\gamma - 60^{\circ}.$

Observe that $A'B_{3}=A'B'$ (due to symmetry) and $C'B_{2}=C'B'.$ It follows that

$s=\alpha +\gamma - 30^{\circ}$

and

$2h+2\alpha +2\gamma=180^{\circ},$

hence $h=\angle B_{2}B{3}B'=\angle B'B_{2}B_{3}.$ Consequently, we have $h=90^{\circ}-\alpha -\gamma,$ thus

$\begin{align} h - s &= 120^{\circ}-2\alpha -2\gamma\\ &= 120^{\circ}-\frac{2}{3}(3\alpha +3\gamma)\\ &= 120^{\circ}-\frac{2}{3}(180^{\circ}-3\beta)\\ &= 2\beta, \end{align}$

and thus $u=2b,$ where $u=\angle B_{2}B_{3}A'=\angle SB_{2}B_{3}.$ At this point, we observe that

$B_{2}A'=A'C'=C'B_{2}$

because of the isosceles triangle $A'B'C',$ and thus

$\begin{align} \angle B_{3}C'B_{2} &= 180^{\circ}-u-\frac{u}{2}\\ &= 180^{\circ}-\frac{3u}{2}\\ &= 180^{\circ}-3\beta. \end{align}$

It follows that the quadrilateral $B_{3}C'B_{2}$ is inscribed in a circle, and similarly, we obtain that the quadrilateral $BB_{2}A'B_{3}$ can be inscribed in a circle, as well. Consequently the straight lines $BA',$ $BC'$ trisect $\angle ABC,$ hence $T=A'$ and $S=C'.$

References

1. S. E. Louridas, M. Th. Rassias, Problem-Solving and Selected Topics in Euclidean Geometry, Springer, 2013 (65-68)

Morley's Miracle

On Morley and his theorem

1. Doodling and Miracles
2. Morley's Pursuit of Incidence
3. Lines, Circles and Beyond
4. On Motivation and Understanding
5. Of Looking and Seeing

Backward proofs

1. J.Conway's proof
   • Remarks on J. Conway's proof
2. D. J. Newman's proof
3. B. Bollobás' proof
4. G. Zsolt Kiss' proof
5. Backward Proof by B. Stonebridge
6. Morley's Equilaterals, Spiridon A. Kuruklis' proof
7. J. Arioni's Proof of Morley's Theorem

Trigonometric proofs

1. Bankoff's proof
2. B. Bollobás' trigonometric proof
3. Proof by R. J. Webster
4. A Vector-based Proof of Morley's Trisector Theorem
5. L. Giugiuc's Proof of Morley's Theorem
6. Dijkstra's Proof of Morley's Theorem

Synthetic proofs

1. Another proof
2. Nikos Dergiades' proof
3. M. T. Naraniengar's proof
4. An Unexpected Variant
5. Proof by B. Stonebridge and B. Millar
6. Proof by B. Stonebridge
7. Proof by Roger Smyth
8. Proof by H. D. Grossman
9. Proof by H. Shutrick
10. Original Taylor and Marr's Proof of Morley's Theorem
11. Taylor and Marr's Proof - R. A. Johnson's Version
12. Morley's Theorem: Second Proof by Roger Smyth
13. Proof by A. Robson

Algebraic proofs

1. Morley's Redux and More, Alain Connes' proof

Invalid proofs

1. Bankoff's conundrum
2. Proof by Nolan L Aljaddou
3. Morley's Theorem: A Proof That Needs Fixing

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny