Morley's Theorem
Roger Smyth
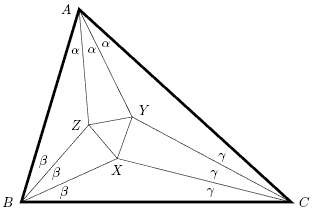
Morley's theorem asserts that in the diagram below the triangle XYZ is equilateral, whatever ΔABC.
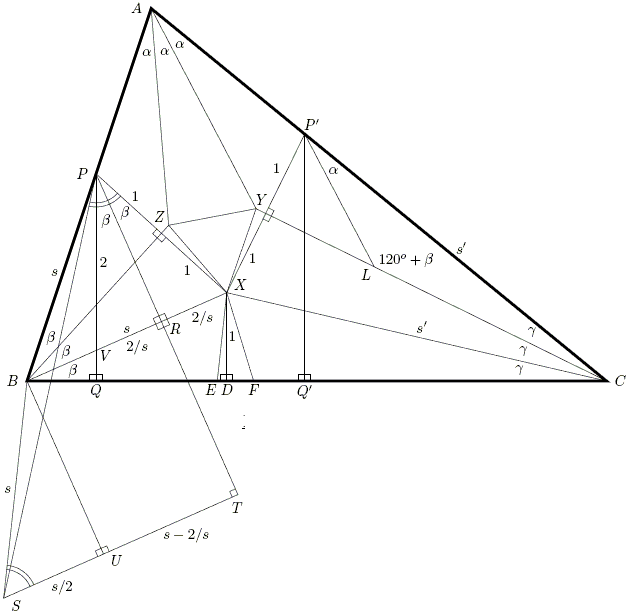
In the next diagram, the unit of measure is the perpendicular DX, and the lengths of BX and CX are s and s'. E and F are points on BC where ∠CEX = 60° + β and
∠XFB = 60° + γ. P and P' are where BP = s and CP' = s' and S is constructed so that BS = s and SBX = 120°. This makes the two marked angles (TSB and SPX) 60°. The rest of the construction is hopefully as self-explanatory.
What can be said of the diagram?
| |
- α + β + γ = 60° (so ∠EXF = α)
- ∠CYA = ∠CLP' = 120° + β
- ∠TSB = ∠SPX = 60°
- AY = (AC/s')LP' (for, ΔCP'L is similar to ΔCAY)
- LP' = PS/ST (for ∠P'LY = ∠SPT = 60° - β)
- XR = RV = 2/s (for triangles BDX, PRX, PVR are similar)
- SU = s/2 (for ∠BSU = 60°)
| |
Now, by (vi) and (vii),
| |
2 ST = 2 SU + 2 UT = s + 2(s - 2/s) = 3s - 4/s.
| |
Also, since triangles BQV and BDX are similar, VQ = 1 - 4/s² so
leading to 2 ST = s PQ.
Next, by (iv) and (v),
| |
AY = (AC / s')(PS / ST) = 2 AC·PS / (ss' PQ).
| |
But XE = 2s/PS as ΔPBS is isosceles and ∠SBP = 2(60° + β) = 2∠DEX. It follows that
and, by symmetry,
| |
(XE·AY) / (XF·AZ) = [4 AC / (s' PQ)] [(s P'Q') / (4 AB)] = (s AC·P'Q') / (s' AB·PQ) = 1
| |
because PQ(AB/s) = P'Q'(AC/s') is the altitude of ΔABC. However, this means AZ / AY = XE / XF which together with ∠ZAY = α = ∠EXF implies that triangles AZY and XEF are similar. Hence ∠YZA = ∠FEX = 60° + β and ∠AYZ = ∠XFE = 60° + γ. Analogous arguments for ΔBXZ and ΔCYX give ∠ZXB = 60° + γ, ∠CXY = 60° + β and ∠BZX = ∠CYX = 60° + α. All the angles in the diagram may now be deduced in terms of α, β, γ and it transpires that every angle of ΔXYZ is 60°.
References
- M. R. F. Smyth, MacCool's proof of Morley's Miracle, Irish Math. Soc. Bulletin 63 (2009), 63-66
- J.Conway's proof
- D. J. Newman's proof
- Bankoff's proof
- B. Bollobás' proof
- Another proof
- Nikos Dergiades' proof
- G. Zsolt Kiss' proof
- M. T. Naraniengar's proof
- Doodling and Miracles
- Morley's Pursuit of Incidence
- Lines, Circles and Beyond
- On Motivation and Understanding
- Bankoff's conundrum
- Of Looking and Seeing
- Morley's Redux and More, Alain Connes' proof
- An Unexpected Variant
- Proof by B. Stonebridge and B. Millar
- Proof by B. Stonebridge
- Proof by Nolan L Aljaddou
- Proof by Roger Smyth
- Proof by H. D. Grossman
- Proof by R. J. Webster
Copyright © 1996-2010 Alexander Bogomolny
|
