Morley's Theorem, a Proof
Brian Stonebridge 2009
In the diagram below, the near trisectors of the internal angles at the vertices $A,$ $B,$ and $C$ of a triangle meet in $X,$ $Y,$ and $Z.$ Morley's theorem states that the triangle $XYZ$ is equilateral.
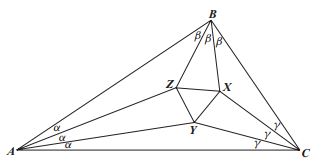
Using the notation in the diagram, since, in $\Delta ABC, $3\alpha + 3\beta + 3\gamma = \pi ,$
$\alpha + \beta + \gamma = \pi /3.$
Start with an arbitrary equilateral triangle $XYZ.$.
Let $P,$ $Q,$ $R$ be point on the altitudes $\Delta XYZ$ (produced) such that
$\displaystyle\angle XPY=\angle XPZ=\alpha+\frac{\pi}{6},\\ \angle YQZ=\angle YQX=\beta+\frac{\pi}{6},\\ \angle ZRX=\angle ZRY=\gamma+\frac{\pi}{6}. $
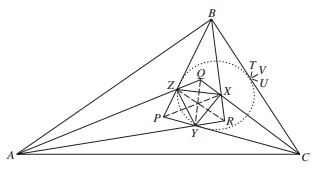
Define $A$ to be the intersection of $QZ$ and $RY,$ $B$ the intersection of $RX$ and $PZ,$ and $C$ that of $PY$ and $QX.$ Then in quadrilateral $XRAQ,$ $\displaystyle\angle AQX=2\beta +\frac{\pi}{3},$ $\displaystyle\angle ARX=2\gamma +\frac{\pi}{3},$ and $\displaystyle\angle QXR=2\alpha +\beta +\gamma+\frac{\pi}{3}.$ It follows that $\angle ZAY=\alpha.$ Similarly, $\angle XBZ =\beta$ and $\angle YCX=\gamma.$
Draw circle with center $X$ touching $PB$ and, since $PX$ bisects $\angle BPC,$ it also touches $PC.$ Next, draw tangents $BT$ and $CU$, set $V$ as the intersection of the two lines. Then,
$\angle XBT=\angle XBZ=\beta$ and $\angle XCU =\angle XCY=\gamma.$
Now, the sum of angles $P,$ $B,$ and $C$ in quadrilateral $PBVC$ equals
$\displaystyle\angle QXR=2\alpha+\frac{\pi}{3} +2\beta +2\gamma=\pi,$
implying that $\angle TVU=0.$ In other words, $BTVUC$ is a straight line so that $T$ and $U$ coincide in $V.$ It follows that $\angle XBC=\beta$ and $\angle XCB=\gamma.$ In the same manner the angles of triangles $YCA$ and $ZAB$ are determined, letting one to conclude that triangle $ABC$ has angles $3\alpha,$ $3\beta,$ and $3\gamma.$ It may be scaled (if need be) to coincide with the original triangle.
- B. Stonebridge, A Simple Geometric Proof of Morley's Trisector Theorem, Applied Probability Trust, 2009
Morley's Miracle
On Morley and his theorem
- Doodling and Miracles
- Morley's Pursuit of Incidence
- Lines, Circles and Beyond
- On Motivation and Understanding
- Of Looking and Seeing
Backward proofs
- J.Conway's proof
- D. J. Newman's proof
- B. Bollobás' proof
- G. Zsolt Kiss' proof
- Backward Proof by B. Stonebridge
- Morley's Equilaterals, Spiridon A. Kuruklis' proof
- J. Arioni's Proof of Morley's Theorem
Trigonometric proofs
- Bankoff's proof
- B. Bollobás' trigonometric proof
- Proof by R. J. Webster
- A Vector-based Proof of Morley's Trisector Theorem
- L. Giugiuc's Proof of Morley's Theorem
- Dijkstra's Proof of Morley's Theorem
Synthetic proofs
- Another proof
- Nikos Dergiades' proof
- M. T. Naraniengar's proof
- An Unexpected Variant
- Proof by B. Stonebridge and B. Millar
- Proof by B. Stonebridge
- Proof by Roger Smyth
- Proof by H. D. Grossman
- Proof by H. Shutrick
- Original Taylor and Marr's Proof of Morley's Theorem
- Taylor and Marr's Proof - R. A. Johnson's Version
- Morley's Theorem: Second Proof by Roger Smyth
- Proof by A. Robson
Algebraic proofs
Invalid proofs
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73509596
