Sine, Cosine, and Ptolemy's Theorem

Ptolemy's theorem implies the theorem of Pythagoras. The latter serves as a foundation of Trigonometry, the branch of mathematics that deals with relationships between the sides and angles of a triangle. In the language of Trigonometry, Pythagorean Theorem reads

where A is one of the internal angles of a right triangle. If the hypotenuse of the triangle is of length 1, then sin(A) is the length of the side opposite to the angle A, cos(A) is the length of the adjacent side.

Ptolemy's theorem also provides an elegant way to prove other trigonometric identities. In a little while, I'll prove the addition and subtraction formulas for sine:

But first let's have a simple proof for the Law of Sines.

Proposition III.20 from Euclid's Elements says:

The more common formulation asserts that an angle circumscribed in a circle is equal to half the central angle that subtends the same chord. (As a corollary, from here it follows that all circumscribed angles subtending the same arc are equal irrespective of their position on the circle. This is Proposition III.21) On the diagram, ∠BOC = 2∠BAC (= 2A.)

Drop a perpendicular from O on the side BC. Assuming the radius of the circle is R, OB = OC = R. Also, ∠BOP = ∠POC. In ΔBOP, sin(∠BOP) = BP/OB = BC/2R. Therefore, BC/sin(∠BOP) = 2R. When angle A is obtuse, the center O is located outside ΔABC and the diagram looks differently. The resulting identity is, however, the same. Repeating these steps with the other two angles B and C of ΔABC we get the Law of Sines which in the standard notations appear as

(3)	a sin(A) = b sin(B) = c sin(C) = 2R

In the case, where the diameter of the circumscribed circle is 1, we have a = sin(A), b = sin(B), and c = sin(C). This is all we need to apply Ptolemy's theorem. This is of course useful to remember the definition of the sine and cosine functions. In a right triangle, the sine of an acute angle is the ratio of the opposite leg to the hypotenuse; its cosine is the ratio of the adjacent leg to the hypotenuse.

Consider a quadrilateral ABDC inscribed into a circle of diameter 1 so that the diagonal BC serves as a diameter.

From the definition of sine and cosine we determine the sides of the quadrilateral. The Law of Sines supplies the length of the remaining diagonal. The addition formula for sine is just a reformulation of Ptolemy's theorem.

To prove the subtraction formula, let the side BC serve as a diameter.

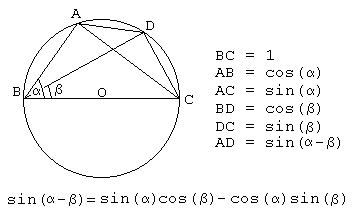
As a consequence, we obtain formulas for sine (in one step) and for cosine (in two steps) of complementary angles:

From these and the addition formulas for sine it is not difficult to derive the addition formulas for cosine:

(There are additional simple proofs of those formulas.)

References

1. E. Maor, Trigonometric Delights, Princeton University Press, 1998

Trigonometry

• What Is Trigonometry?
• Sine of a Sum Formula
• Addition and Subtraction Formulas for Sine and Cosine
• Addition and Subtraction Formulas for Sine and Cosine II
• The Laws of Cosines
• The Law of Sines and Cosines
• Cosine of 36 degrees
• Sine, Cosine, and Ptolemy's Theorem
• arctan(1) + arctan(2) + arctan(3) = π
• arctan(1/2) + arctan(1/3) = arctan(1)
• Morley's Miracle
• Napoleon's Theorem

Copyright © 1996-2010 Alexander Bogomolny