One of the sad things about the current philosophy of mathematical education is the avoidance of plane geometry. Today's generation, and perhaps their parents as well have not heard of marvels like the 9-point circle, Descartes's theorem, Ceva's Theorem, or the marvel of marvels, the Morley triangle.

As shown in Figure 1, one takes an arbitrary triangle and trisects its angles, obtaining three intersection points. These form the small triangle inside the starting triangle. This small interior triangle is far from being arbitrary, however, Morley's great discovery (1899) being that it is always equilateral!

When I read, or rather tried to read, Morley's proof of this startling theorem, I found it absolutely impenetrable. I told myself that maybe in future years I would return and then understand it. I never succeeded in that, and even when I read the much simpler proof based on trigonometry, or the fairly simple geometric proof due to M. T. Naraniengar (c 1907), there was still too much complexity and lack of motivation. (A series of lucky breaks!) Were we to give up, forever, understanding the Morley Miracle? Or are we failing because we are asking too little? After all, Morley's theorem states that in Figure 1, the inner triangle always will be equilateral. The reason that all the proofs seem to be so difficult and unmotivated is probably because Morley's theorem is really only half the story. The full picture is in Figure 1 and this tells the whole story and indeed proves itself! (This happens often in induction proofs: The fuller statement is easier to prove than the restricted one.)

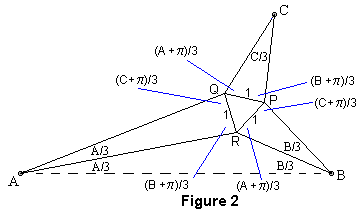
So we turn to the "cheating" strategy as used in [4], namely, we start with the equilateral triangle and build out. The result is Figure 2. Here we have normalized matters by choosing the equilateral triangle to have side 1. Note that from symmetry it will be sufficient to prove that the indicated angle is A/3.

At this point we could turn the proof over to a high school trigonometry student who has learned to "solve triangles." Observe that all the side lengths in Figure 2 are determined by angle-side-angle (ASA) of the three constructed triangles. Thus, the law of sines applied to triangle AQR gives

so

Similarly,

Also

∠ARB = 2π - (A + π)/3 - (B + π)/3 - π/3 = (C + 2π)/3,

so for triangle ARB we have Figure 3.

For this triangle we know two sides and the included angle, (SAS), so the remaining angles are determined, and they must be A/3 and B/3, which one verifies by once again using the law of sines. Q.E.D.

References

1. D. Gale, Tracking the Automatic Ant, Springer, 1998
2. J. M. Child, A Proof of Morley's Theorem, The Math. Gaz. (1922), 171.
3. H. S. M. Coxeter, Introduction to Geometry, Toronto: John Wiley and Sons (1969), pp. 23-25.
4. Frank Morley, Extensions of Clifford's theorem, Amer. J. Math. 51 (1929), 465-472.
5. M. T. Navansiengar, Educ. Times, New Series 15 (1909), 47.