Tony Foster's Proof of Viviani's Theorem
What Might This Be About?
23 February, 2017, Created with GeoGebra
Viviani's Theorem
The sum of distances of a point inside an equilateral triangle or on one of its sides equals the length of its altitude.
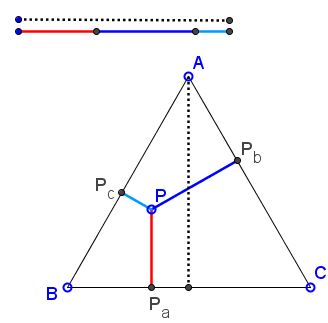
The theorem is named after Vincenzo Viviani (1622-1703).
Proof
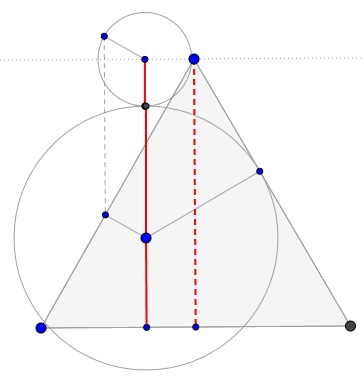
Acknowledgment
The above is a slight modification of Tony Foster's proof of Viviani's theorem.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73573617
