Morley's Theorem, a Proof

Brian Stonebridge (University of Bristol, UK)
January 30, 2009

In the diagram below, the near trisectors of the internal angles at the vertices A, B, and C of a triangle meet in X, Y, and Z. Morley's theorem states that the triangle XYZ is equilateral. We give here a direct Euclidean proof.

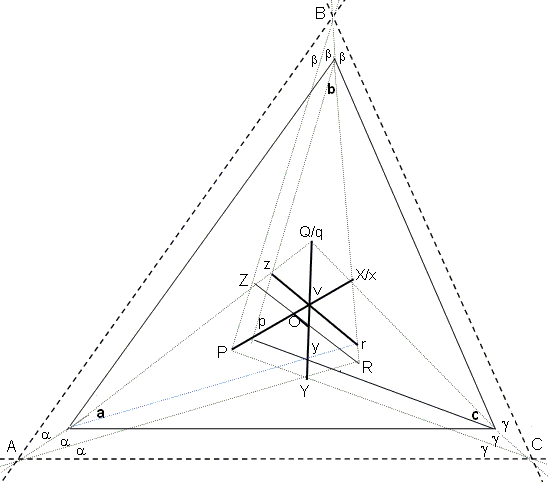
Using the notation in the diagram, since, in ΔABC, 3α + 3β + 3γ = π,

(1)	α + β + γ = π/3.

From triangles BPC, CQA, ARB,

(2)	∠BPC = 2(α + π/6) ∠CQA = 2(β + π/6) ∠ARB = 2(γ + π/6)

Observe that, in ΔBPC, X is the intersection of the bisectors of angles at B and C. It follows that PX is the bisector of the angle at P. Thus,

(3)	∠ROX = ∠OPY + ∠ORY - ∠RYC = (α + π/6) + (β + π/6) - (γ + π/6) = π/3.

This result holds for any other pair of diagonals PX, QY, RZ.

Assume that the diagonals are not concurrent, and thus form a triangle.

Select a diagonal, RZ, say, and, through the opposite vertex v, draw rz, parallel to RZ, with z, r on QA, RB. Then, Δzvq, Δxvq are congruent (ASA). Choose y, p so that Δxvr, Δyvr are congruent (ASA) making

(4)	vz = vx = vy,

and ∠vpy = ∠OPY so that Δvpy, Δvpz are congruent (SAA). Then the angles of pzqxry, PZQXRY are the same.

Joining opposite sides of pzqxry we obtain Δabc, with angles 3α, 3β, 3γ and its trisectors which generate Δxyz.^** Triangles abc / ABC are similar, but, in Δabc, the diagonals are concurrent whilst in ΔABC they are not. This contradiction implies that our original assumption of non-concurrence of the diagonals of PZQXRY was false, and they must be concurrent. In pzqxry, we deduce from (3) and (4) that Δxyz is an equilateral triangle (equal radii, equal angles 2π/3).

** Informally," the mapping pzqxry ↔ abc is 1-1" suffices, but more formally the derivation of this result is as follows:

The intersections of opposite sides of pzqxry give Δabc. Since ∠zbx = β, if we draw a line at β to bz through b, bz is the bisector of the angle at b. But, rz (the bisector at r) meets bz at z, so z is the incenter of the triangle, T, say (with vertices b, r, and a third vertex at a, angle 2α with ry). Thus, its bisector az must make angle α with ry. But ra lies along ry and ∠zar = α, so the point, a, completes T. Repeating this argument, the angles of Δabc are seen to be trisected.

Morley's Miracle

On Morley and his theorem

1. Doodling and Miracles
2. Morley's Pursuit of Incidence
3. Lines, Circles and Beyond
4. On Motivation and Understanding
5. Of Looking and Seeing

Backward proofs

1. J.Conway's proof
   • Remarks on J. Conway's proof
2. D. J. Newman's proof
3. B. Bollobás' proof
4. G. Zsolt Kiss' proof
5. Backward Proof by B. Stonebridge
6. Morley's Equilaterals, Spiridon A. Kuruklis' proof
7. J. Arioni's Proof of Morley's Theorem

Trigonometric proofs

1. Bankoff's proof
2. B. Bollobás' trigonometric proof
3. Proof by R. J. Webster
4. A Vector-based Proof of Morley's Trisector Theorem
5. L. Giugiuc's Proof of Morley's Theorem
6. Dijkstra's Proof of Morley's Theorem

Synthetic proofs

1. Another proof
2. Nikos Dergiades' proof
3. M. T. Naraniengar's proof
4. An Unexpected Variant
5. Proof by B. Stonebridge and B. Millar
6. Proof by B. Stonebridge
7. Proof by Roger Smyth
8. Proof by H. D. Grossman
9. Proof by H. Shutrick
10. Original Taylor and Marr's Proof of Morley's Theorem
11. Taylor and Marr's Proof - R. A. Johnson's Version
12. Morley's Theorem: Second Proof by Roger Smyth
13. Proof by A. Robson

Algebraic proofs

1. Morley's Redux and More, Alain Connes' proof

Invalid proofs

1. Bankoff's conundrum
2. Proof by Nolan L Aljaddou
3. Morley's Theorem: A Proof That Needs Fixing

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny