Morley's Miracle
A. Robson's Proof
Theorem
The three points of intersection of the adjacent trisectors of the angles of any triangle form an equilateral triangle.
Proof
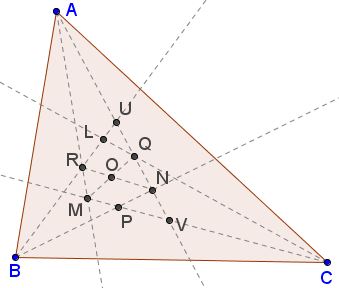
With a reference to the diagram, let $BRL\;$ cut $AQ\;$ in $U;\;$ $AQ\;$ produced cuts $BP\;$ in $N\;$ and $CP\;$ in $V;\;$ $CP\;$ cuts $AR\;$ in $M;\;$ $QM\;$ cuts $RN\;$ in $O.\;$
Then $BP,\;BL\;$ are isogonal, and so are $CP,\;CL.\;$ It follows that $AL,\;AP\;$ are also isogonal. Further, $A(BRLU)=A(CVPM).\;$ Hence,
$N(BRLU)=Q(CVPM)=Q(PMCV),$
and these pencils have a common ray. Therefore, their corresponding rays have collinear intersections, implying that $P,\;$ $O,\;$ $L,\;$ are collinear.
As $R\;$ is the incenter of $\Delta ANB,\;$ $\angle ARN=90^{\circ}+\frac{1}{3}B.\;$
As $Q\;$ is the incenter of $\Delta AMC,\;$ $\angle RMQ=90^{\circ}-\frac{1}{3}A-\frac{1}{3}C,\;$
so that the difference, viz., $\angle ROM=60^{\circ}.\;$ Similarly, the other angles at $O\;$ are $60^{\circ};\;$ since they have a common base and equal angles at each of its extremities, the triangles $ORL\;$ and $OQL\;$ are congruent, and so are the triangles $PRL,\;PQL,$ making $\Delta PQR\;$ equilateral.
Eurika's Editor's notes on Robson's proof
The proof uses the idea of isogonal rays. If two rays through the vertex of an angle make equal angles with its sides, they are said to be isogonal. They are then mirror images in the bisector of the angle. The theorem used by Robson on isogonals is:
If three lines from the vertices of a triangle are concurrent, their isogonals are also concurrent.
He then uses the idea of projective pencils, pencils with equal cross-ratios, and the theorem that if two projective pencils with distinct vertices have a self-corresponding ray, the three intersections of corresponding rays are collinear. He also uses the theorem that in a cross-ratio the interchange of a pair of elements together with the interchange of the other pair does not affect the value of the cross-ratio. Robson's proof is as short as anyone could desire, and it avoids elaborate initial constructions.
Acknowledgment
I am deeply indebted to Roger Smyth for bringing the 1978 Eurika's issue cited below to my attention.
References
- A. Robson, The Mathematical Gazette, 1922-1923, pp 310-311
- A. Robson, Eurika, v 3, n 10, 1978, p 280
Morley's Miracle
On Morley and his theorem
- Doodling and Miracles
- Morley's Pursuit of Incidence
- Lines, Circles and Beyond
- On Motivation and Understanding
- Of Looking and Seeing
Backward proofs
- J.Conway's proof
- D. J. Newman's proof
- B. Bollobás' proof
- G. Zsolt Kiss' proof
- Backward Proof by B. Stonebridge
- Morley's Equilaterals, Spiridon A. Kuruklis' proof
- J. Arioni's Proof of Morley's Theorem
Trigonometric proofs
- Bankoff's proof
- B. Bollobás' trigonometric proof
- Proof by R. J. Webster
- A Vector-based Proof of Morley's Trisector Theorem
- L. Giugiuc's Proof of Morley's Theorem
- Dijkstra's Proof of Morley's Theorem
Synthetic proofs
- Another proof
- Nikos Dergiades' proof
- M. T. Naraniengar's proof
- An Unexpected Variant
- Proof by B. Stonebridge and B. Millar
- Proof by B. Stonebridge
- Proof by Roger Smyth
- Proof by H. D. Grossman
- Proof by H. Shutrick
- Original Taylor and Marr's Proof of Morley's Theorem
- Taylor and Marr's Proof - R. A. Johnson's Version
- Morley's Theorem: Second Proof by Roger Smyth
- Proof by A. Robson
Algebraic proofs
Invalid proofs
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1966-2016 Alexander Bogomolny
73572027
