A Sangaku with an Egyptian Attachment: What Is This About?
A Mathematical Droodle

Solution

Copyright © 1996-2009 Alexander Bogomolny

The applet purports to suggest the following sangaku [Temple Geometry, p. 3]:

(This is a Sangaku from the Miyagi prefecture whose tablet has disappeared long ago.)

We already met this configuration and now how to compute the radius and location of circle Q. If the radii of the circles on A and B are R₁ and R₂, the radius of circle Q r and the horizontal distances between the left circle and Q and Q and the right circle are x and y then

However, from (1), xy = 2r(x + y), which transforms (2) into

or

It's not hard to see that the only right triangle in which twice one leg equals the sum of the hypotenuse and the other leg are equal is the famous 3-4-5 triangle, often referred to as the Egyptian triangle. Indeed, let a, b, c be the legs and the hypotenuse of a right triangle that satisfy say

and then (3) implies

If we define t = a/3, then

This tells us that R and H and hence O do not depend on the values of x and y but only on their sum (x + y) and are invariant for a fixed pair of points A and B.

Applying inversion Michel Cabart found a shorter solution to the problem:

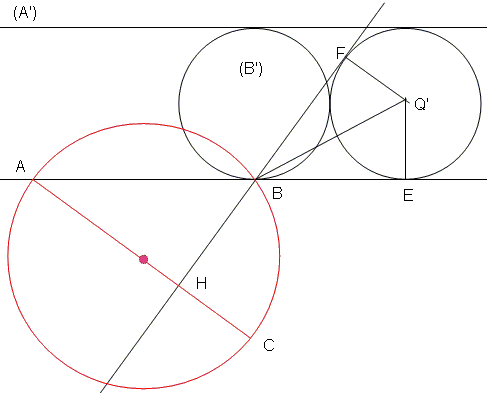
Let's transform the figure by an inversion with center A letting point B invariant. Then

• line (AB) is globally invariant,
• circle (A) becomes line (A') parallel to (AB),
• circle (B) becomes circle (B') tangent to (AB) in B and to line (A'),
• circle (Q) becomes circle (Q') tangent to (B') and to lines (A') and (AB), thus equal to (B').

The tangent (BF) to circle (Q') satisfies: tan (FBE/2) = t = 1/2. Its position is thus fixed. It is the inverse of a fixed circle in the original figure passing by A and B (red) and tangent to circle (Q). In this circle we have: AH × AC = AB² (as H is the inverse of C) or 2R x sin FBE = AB; but sin FBE = 2t/(1+t2) = 4/5. Thus R = (5/8)AB.

References

1. H. Fukagawa, D. Pedoe, Japanese Temple Geometry Problems, The Charles Babbage Research Center, Winnipeg, 1989

   Write to:

   Charles Babbage Research Center
   P.O. Box 272, St. Norbert Postal Station
   Winnipeg, MB
   Canada R3V 1L6

Sangaku

1. Sangaku: Reflections on the Phenomenon
2. Critique of My View and a Response
3. 1 + 27 = 12 + 16 Sangaku
4. 3-4-5 Triangle by a Kid
5. 7 = 2 + 5 Sangaku
6. A 49^th Degree Challenge
7. A Geometric Mean Sangaku
8. A Hard but Important Sangaku
9. A Restored Sangaku Problem
   • A better solution to a difficult sangaku problem
10. A Sangaku: Two Unrelated Circles
11. A Sangaku by a Teen
12. A Sangaku Follow-Up on an Archimedes' Lemma
13. A Sangaku with an Egyptian Attachment
14. A Sangaku with Many Circles and Some
15. A Sushi Morsel
16. An Old Japanese Theorem
17. Archimedes Twins in the Edo Period
18. Arithmetic Mean Sangaku
19. Bottema Shatters Japan's Seclusion
20. Circles and Semicircles in Rectangle
21. Circles in a Circular Segment
22. Circles Lined on the Legs of a Right Triangle
23. Equal Incircles Theorem
24. Equilateral Triangle, Straight Line and Tangent Circles
25. Equilateral Triangles and Incircles in a Square
26. Five Incircles in a Square
27. Four Hinged Squares
28. Four Incircles in Equilateral Triangle
29. Gion Shrine Problem
30. Harmonic Mean Sangaku
31. Heron's Problem
32. In the Wasan Spirit
33. Incenters in Cyclic Quadrilateral
34. Japanese Art and Mathematics
35. Malfatti's Problem
36. Maximal Properties of the Pythagorean Relation
37. Neuberg Sangaku
38. Out of Pentagon Sangaku
39. Peacock Tail Sangaku
40. Pentagon Proportions Sangaku
41. Pythagoras and Vecten Break Japan's Isolation
42. Radius of a Circle by Paper Folding
43. Review of Sacred Mathematics
44. Sangaku à la V. Thebault
45. Sangaku and The Egyptian Triangle
46. Sangaku in a Square
47. Sangaku Iterations, Is it Wasan?
48. Sangaku with 8 Circles
49. Sangaku with Three Mixtilinear Circles
50. Sangaku with Versines
51. Sangakus with a Mixtilinear Circle
52. Sequences of Touching Circles
53. Square and Circle in a Gothic Cupola
54. Tangent Circles and an Isosceles Triangle
55. The Squinting Eyes Theorem
56. Steiner's Sangaku
57. Three Incircles In a Right Triangle
58. Three Squares and Two Ellipses
59. Three Tangent Circles Sangaku
60. Triangles, Squares and Areas from Temple Geometry
61. Two Arbelos, Two Chains
62. Two Circles in an Angle
63. Two Sangaku with Equal Incircles

Copyright © 1996-2009 Alexander Bogomolny