Pinning Butterfly on Radical Axes

The applet below illustrates a solution to the traditional Butterfly Problem that was communicated to me by Giles Gardam, a member of Australia's 2007 and 2008 IMO teams, and is due to his mentor, Ivan Guo, who won a gold medal at IMO 2004.

In a circle T, two chords AB and CD intersect at the midpoint of a third chord PQ. AD meets PQ in X, BC meets PQ in Y. The task is to show that M is also the midpoint of XY.

---

Among the many browsers currently available, the Firefox is the one that - with sufficient permissions - still runs Java.

---

What if applet does not run?

Reflect B and C and the circle T in M (by reflect in a point I mean a dilation by factor -1 about that point). B', C', and T' be the reflections of B, C and circle T, respectively. Note that as M is the midpoint of PQ, T' passes through P and Q.

By power of point M with respect to T, AM×BM=CM×DM.

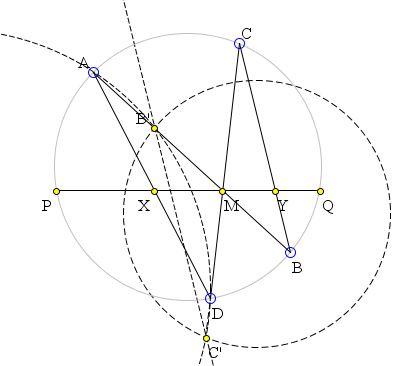
Thus AM×B'M=C'M×DM, so by converse of power of a point, AB'C'D is a cyclic quadrilateral. Let its circumcircle be T''.

We now consider the three radical axes of the three circles, which are PQ, AD and B'C', and concur by the radical axes theorem. Thus B'C' intersects PQ at X. The reflections of BC and PQ are B'C' and PQ, so considering their intersections, we have that X is the reflection of Y, thus M is the midpoint of XY.

Butterfly Theorem and Variants

1. Butterfly theorem
2. 2N-Wing Butterfly Theorem
3. Better Butterfly Theorem
4. Butterflies in Ellipse
5. Butterflies in Hyperbola
6. Butterflies in Quadrilaterals and Elsewhere
7. Pinning Butterfly on Radical Axes
8. Shearing Butterflies in Quadrilaterals
9. The Plain Butterfly Theorem
10. Two Butterflies Theorem
11. Two Butterflies Theorem II
12. Two Butterflies Theorem III
13. Algebraic proof of the theorem of butterflies in quadrilaterals
14. William Wallace's Proof of the Butterfly Theorem
15. Butterfly theorem, a Projective Proof
16. Areal Butterflies
17. Butterflies in Similar Co-axial Conics
18. Butterfly Trigonometry
19. Butterfly in Kite
20. Butterfly with Menelaus
21. William Wallace's 1803 Statement of the Butterfly Theorem
22. Butterfly in Inscriptible Quadrilateral
23. Camouflaged Butterfly
24. General Butterfly in Pictures
25. Butterfly via Ceva
26. Butterfly via the Scale Factor of the Wings
27. Butterfly by Midline
28. Stathis Koutras' Butterfly
29. The Lepidoptera of the Circles
30. The Lepidoptera of the Quadrilateral
31. The Lepidoptera of the Quadrilateral II
32. The Lepidoptera of the Triangle
33. Two Butterflies Theorem as a Porism of Cyclic Quadrilaterals
34. Two Butterfly Theorems by Sidney Kung
35. Butterfly in Complex Numbers

Radical Axis and Radical Center

• How to Construct a Radical Axis
• A Property of the Line IO: A Proof From The Book
• Cherchez le quadrilatere cyclique II
• Circles On Cevians
• Circles And Parallels
• Circles through the Orthocenter
• Coaxal Circles Theorem
• Isosceles on the Sides of a Triangle
• Properties of the Circle of Similitude
• Six Concyclic Points
• Radical Axis and Center, an Application
• Radical axis of two circles
• Radical Axis of Circles Inscribed in a Circular Segment
• Radical Center
• Radical center of three circles
• Steiner's porism
• Stereographic Projection and Inversion
• Stereographic Projection and Radical Axes
• Tangent as a Radical Axis
• Two Circles on a Side of a Triangle
• Pinning Butterfly on Radical Axes
• Two Lines - Two Circles
• Two Triples of Concurrent Circles
• Circle Centers on Radical Axes
• Collinearity with the Orthocenter
• Six Circles with Concurrent Pairwise Radical Axes
• Six Concyclic Points on Sides of a Triangle
• Line Through a Center of Similarity

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny