Cut The Knot!

An interactive column using Java applets
by Alex Bogomolny

The Lepidoptera of the Circles

May 2003

The insect order Lepidoptera, with as many as 100,000 species, is second only to the Coleoptera, the beetles. In addition to the familiar butterflies and moths the order includes the skippers, a worldwide group intermediate between butterflies and moths. ... With the exception of a few moths, all adult Lepidoptera have two pairs of wings.

Encyclopædia Britannica

The so called Butterfly Problem has a long history that, according to L. Bankoff, dates back to an 1815 issue of the Gentleman's Diary, an obviously British publication. With forty seven references, Bankoff's article remains the most complete account of the problem up to date. (A few newer references could be found on the Web.) Bankoff ascribes the difficulty in tracing the history of the problem to the fact that the Butterfly appellation made its first appearance as the title of the solutions published in the American Mathematical Monthly in February 1944. Since Howard Eves was at the time the editor of the Elementary Problem Department of the Monthly it is reasonable to assume that he was the first to notice the semblance of the shape in the middle of the problem's diagram to the ubiquitous insect.

Eves' own account has appeared in print twice: as the selection 245° in his Mathematical Circles Revisited and in an interview with D. J. Albers. Eves' language, however, might suggest that this particular butterfly species had been identified earlier. Intrigued by "an elusive and tantalizing little problem in elementary geometry known as the 'butterfly problem'", he ran it as Problem E 571 in the May 1943 issue of the Monthly.

A classic formulation refers to the midpoint of a chord in a circle:


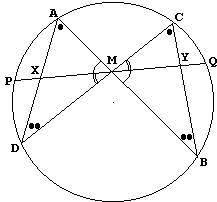(A)	In a circle, M is the midpoint of chord PQ. Chords AB and CD pass through the point M. AD cuts PQ at X, and BC cuts it at Y. Prove that MX = MY.

A generalization does not mention the point M explicitly, nor that it belongs to a chord:

(B)	Given a complete quadrangle inscribed in a circle, if any line cuts two opposite sides at equal distances from the center of the circle, it cuts the other pair of opposite sides at equal distances from the center.

The latter formulation admits lines PQ located away from the circle, the circumstance that may lead an attentive nature observer to discovering additional Lepidoptera families.

If you are reading this, your browser is not set to run Java applets. Try IE11 or Safari and declare the site https://www.cut-the-knot.org as trusted in the Java setup.

Outer Butterfly

Indeed, over the time sightings were reported of various Lepidoptera. The existence of the lopsided butterfly is now a well established fact largely thanks to the efforts of A. Candy (1896). On the other hand, the Three-Winged Butterfly, as appeared in the problem section of the March 1984 issue of Mathematics Magazine, was probably a misnomer. As a matter of fact, the middle bulge in the diagram was very likely just an antennaless head rather than an unmatched wing. In any event, it played no significant role in the problem formulation and could have been done away with. The problem itself was only a particular case of (B). The report, nonetheless, has proved its worth. Among the submitted solutions there were nice generalizations by H. Eves and Jan van de Craats in which the circle, the two pairs of lines AB, CD and AD, BC had been replaced by three arbitrary conics. The new kind of Lepidopteran manifestly deserves the designation of full-curved.

A completely different kind of butterflies was discovered in 1997 by Qiu FaWen, a Chinese mathematics and physics teacher, and his students with the aid of Geometer's Sketchpad. In a recent letter Qiu FaWen pointed me to a web page where he established the existence of a 4-wing butterfly -- a proper Lepidopteran. A paraphrase of his result is now available in English. Due to the exact (4) number of wings expected from a regular butterfly, I feel it appropriate to call Qiu FaWen's result A Better Butterfly Theorem. The letter was followed by another communication -- a Geometer's Sketchpad file -- in which the existence of 2N-wing butterflies has been demonstrated experimentally. The natural habitat of the species is a collection of N circles, not necessarily concentric but having collinear centers. The configuration includes a couple of intersecting lines (spikes) with the point of intersection (nexus) in the interior of all the circles and lying on the line of the centers (spine). A third (classifier) line passes through the nexus perpendicular to the spine. Expeditiously, let's call such a configuration the (2N-wing) butterfly cradle.

The spikes are crossed by the circles in N points on each side of the nexus. 2N-wing butterflies emerge when points on one spike are joined to the points on the other in a 1-1 correspondence. (It must be mentioned that Qiu FaWen has observed even more esoteric varieties, more of the (B) kind.)

If you are reading this, your browser is not set to run Java applets. Try IE11 or Safari and declare the site https://www.cut-the-knot.org as trusted in the Java setup.

2N-wing Butterfly

Below I am going to prove a general statement.

2N-Wing Butterfly Theorem

Observe a 2N-wing butterfly cradle. Let M denote the nexus. Assume the spikes are crossed by the circles in points A_N, ..., A₁, (M), B₁, ..., B_N and C_N, ..., C₁, (M), D₁, ..., D_N, respectively. Let p be any permutation of the index set {1, ..., N}. Finally, for i = 1, ..., N, let X_i and Y_i denote the points where A_iD_p(i) and, respectively, C_iB_p(i) cross the classifier. Then

(1)	1/MX₁ + ... + 1/MX_N = 1/MY₁ + ... + 1/MY_N.

Note that for N = 1 the theorem reduces to (A). The proof depends on two lemmas.

Lemma 1

Let in ΔRST, RU be a cevian through vertex R. Introduce angles a = ∠SRU and b = ∠URT. Then

(2)	sin(a + b)/RU = sin(a)/RT + sin(b)/RS.

The proof is a two-liner that follows from the identity Area( ΔRST) = Area( ΔRSU) + Area( ΔRUT).

Lemma 2 is a curious result in its own right.

Lemma 2

Assume three rays C, B, and Y emanate from point M with Y between C and B. Assume also that, for N > 1, points C₁, ..., C_N have been marked on C, while points B₁, ..., B_N have been marked on B. Let p be any permutation of indices 1, ..., N. Denote the intersection of C_iB_p(i) with Y as Y_i. Then the sum of the reciprocals 1/MY₁ + ... + 1/MY_N does not depend on p.

The proof builds on Lemma 1 which is applied to each of the triangles MC_iB_p(i):

(3)	sin(b + g)/MY_i = sin(g)/MB_p(i) + sin(b)/MC_i,

g and b are the angles CMY and YMB, respectively. Add up all the identities (3). After rearranging the terms, we'll get

(4)	sin(b + g)(1/MY₁ + ... + 1/MY_N) = sin(g)(1/MB₁ + ... + 1/MB_N) + sin(b)(1/MC₁ + ... + 1/MC_N),

in which the right hand side does not depend on the permutation p. The same therefore is true for the left hand side.

Proof of Theorem

The proof easily follows from Lemma 2 by pidgin, or is it pigeon, induction (if a statement holds for N = 1, it holds for any N.) Apply the Butterfly theorem (A) to the i^th circle, i.e the triangles MA_iD_i and MC_iB_i, i = 1, ..., N. If the points of intersection of A_iD_i and C_iB_i with the classifier are denoted as, say, S_i and T_i, (A) assures us that MS_i = MT_i, and therefore 1/MS_i = 1/MT_i. Adding up we get

1/MS₁ + ... + 1/MS_N = 1/MT₁ + ... + 1/MT_N.

But due to Lemma 2,

1/MS₁ + ... + 1/MS_N = 1/MX₁ + ... + 1/MX_N, while
1/MT₁ + ... + 1/MT_N = 1/MY₁ + ... + 1/MY_N,

and the result follows.

Remark 1

The theorem raises further questions. Each permutation can be represented as a product of irreducible cycles. It must be obvious that every such cycle is responsible for forming a unique butterfly. If the permutation is cyclic, the theorem yields a lone insect. However, in general, the N pairs of wings are split between a number of butterflies, one per an irreducible cycle that compose the permutation. This is an open question whether the butterflies are just stuck on top of each other and could be in principle separated, or whether their wings are so entangled that no separation is possible.

L. Bankoff was amazed with a fantastic variety of solutions to the Butterfly problem -- "some by Desargues' theorem on involution, some by the use of cross ratios, others stemming from Menelaus, analytic geometry, trigonometry, advanced Euclidean geometry, and various other modalities ..." Might the braids theory hold the answer to the problem of separation of the entangled butterflies.

Remark 2

In a personal message Douglas Rogers questioned the veracity of the opening Howard Eves story:

... I really wanted to point out that there seems to be something a little strange about Howard Eves' story about the ``Butterfly Theorem''. Not only was the poser of the problem in The American Mathematical Monthly in May, 1943 a Sol Mitchell, of the University of Toronto, the editor of the the Elementary Problems Section was given as H.S.M. Coxeter up until the issue for August/September, 1945, when Howard Eves' name appears in its place. However, Eves was listed among those who also sent in a solution but whose solutions were not reproduced.

Perhaps there is somewhat more to this story than Eves lets on?

References

D. J. Albers, Howard Eves -- The High Elf, in In Eves' Circles, edited by J. M. Anthony, MAA, 1994
L. Bankoff, The Metamorphosis of the Butterfly Problem, Mathematics Magazine, v 60, issue 4 (Oct., 1987), 195-210
H. Eves, Mathematical Circles Revisited, MAA, 2003

Desargues' Theorem

Butterfly Theorem and Variants

71879332