How to Construct a Radical Axis
Given two circles \(A(B)\) and \(C(D)\), with centers at \(A\) and \(C\) and passing through points \(B\) and \(D\), respectively. Below we discuss an Euclidean construction of their radical axis. The radical axis of two circles is the locus of points from which the tangents to the two circles are equal. It can also be defined as the locus of centers of circles simultaneously orthogonal to the given two. The construction is surprisingly simple:
Draw any circle \(C(E,F)\) that intersects both \(A(B)\) and \(C(D)\) - one, say, in points \(G,H,\) the other in points \(I,J.\) Let \(K\) be the intersection of \(GH\) and \(IJ.\) The radical axis of \(A(B)\) and \(C(D)\) is the line through \(K\) perpendicular to the line of centers \(AC\).
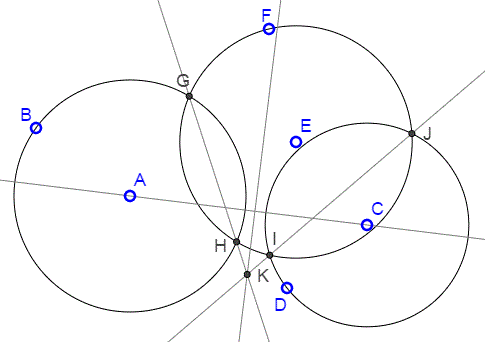
The construction works for any pair of non-concentric circles. There's a good reason to define the line at infinity as the radical axis of two circles that share a center.
The applet below illustrates the construction. Points \(A,B,C,D,E,F\) are draggable.
Why does the construction work? The shortest explanation stems from the transitivity of equality and from the fact that the radical axis of two intersecting circles is the line through the two points of intersection. You can verify the latter by making circles \(A(B)\) and \(C(D)\) intersect. Transitivity implies the existence of the radical center of three circles. Indeed, take two pairs of circles, say \(A(B), E(F)\) and \(C(D), E(F)\). Remarkably, from the point of intersection \(K\) of the two radical axes the tangents to all three circles are equal, implying that that point lies on the third radical axis. By symmetry, the latter is perpendicular to the line \(AB\) of centers. Another short explanation, is based on the Power of a Point, or the Intersecting Chords theorem. Indeed, in circle \(E(F),\) \(KH\cdot KG=KI\cdot KJ\). But the first product is the power of \(K\) with respect to \(A(B)\), while the second product is the power of \(K\) with repsect to \(C(D)\).
So, this is what you see in the applet. However, within the applet, the construction is implemented as a sequence of algebraic steps. Below I explain how.
For the sake of calculations I choose a special circle \(E(F)\). To emphasize the properties of that circle, I change the notations. The center \(L\) of the circle is a point on the radical axis of \(A(B)\) and \(C(D).\) The circle is chosen to be orthogonal to both \(A(B)\) and \(C(D).\) Let \(LN\) and \(LP\) be tangent to \(A(B)\) and \(LM\) and \(LR\) \(C(D).\) Since \(L\) is ont the radical axis of \(A(B)\) and \(C(D),\) all four segments are equal such that the points \(M,N,P,R\) are concyclic with center at \(L\). Their circlumcircle is orthogonal to both \(A(B)\) and \(C(D)\) because, for example, \(CM\perp LM\).
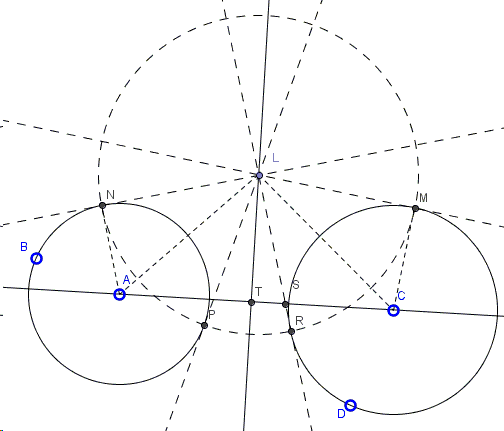
Let \(T\) be the foot of the perpendicular from \(L\) to \(AB\). This point is at the heart, or rather the goal, of the calculations because the perpendicular to \(AC\) at \(T\) is exactly the radical axis of \(A(B)\) and \(C(D).\) By several applications of the Pythagorean theorem,
\( LN^{2}+AN^{2}=AL^2=AT^{2}+LT^{2} \\ LM^{2}+CM^{2}=CL^2=CT^{2}+LT^{2}. \)
The difference of the two equation yields
\( AN^{2}-CM^{2}=AT^{2}-CT^{2}=AC\cdot (AT-CT), \)
for, as was pointed out, \(LM=LN\). Thus we have a system:
\(\displaystyle AT-CT=\frac{AN^{2}-CM^{2}}{AC} \\ AT+CT=AC, \)
from which, \(\displaystyle AT = \frac{1}{2}\bigg(\frac{AN^{2}-CM^{2}}{AC}+AC\bigg).\)
Radical Axis and Radical Center
- How to Construct a Radical Axis
- A Property of the Line IO: A Proof From The Book
- Cherchez le quadrilatere cyclique II
- Circles On Cevians
- Circles And Parallels
- Circles through the Orthocenter
- Coaxal Circles Theorem
- Isosceles on the Sides of a Triangle
- Properties of the Circle of Similitude
- Six Concyclic Points
- Radical Axis and Center, an Application
- Radical axis of two circles
- Radical Axis of Circles Inscribed in a Circular Segment
- Radical Center
- Radical center of three circles
- Steiner's porism
- Stereographic Projection and Inversion
- Stereographic Projection and Radical Axes
- Tangent as a Radical Axis
- Two Circles on a Side of a Triangle
- Pinning Butterfly on Radical Axes
- Two Lines - Two Circles
- Two Triples of Concurrent Circles
- Circle Centers on Radical Axes
- Collinearity with the Orthocenter
- Six Circles with Concurrent Pairwise Radical Axes
- Six Concyclic Points on Sides of a Triangle
- Line Through a Center of Similarity
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73573195
