Stereographic Projection and Radical Axes
Hubert Shutrick
|
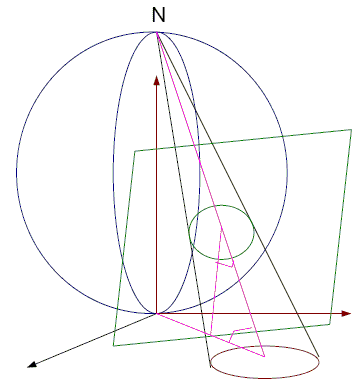
A sphere rests on the xy-plane at the origin O and N is its top point on the z-axis. Projection from N of the sphere onto the xy-plane is called stereographic projection. More generally, stereographic projection maps a sphere to any plane with a pencil of lines through a selected point on the sphere that does not belong to the plane of projection but lies on the diameter of the sphere perpendicular to the plane. In particular, the center of the sphere may be made to coincide with the origin. Regardless of the choice of the point and the planes, stereographic projection possesses several important properties. Below we shall assume that a sphere rests on the plane of projection with N the highest point.
Theorem
Stereographic projection preserves angles.
It takes circles on the sphere that pass through N onto lines in the xy-plane and is a one-to-one correspondence between them (an interactive illustration of this fact is available on a separate page.)
It takes circles on the sphere that don't pass through N onto circles in the xy-plane and is a one-to-one correspondence between them.
Proof
|
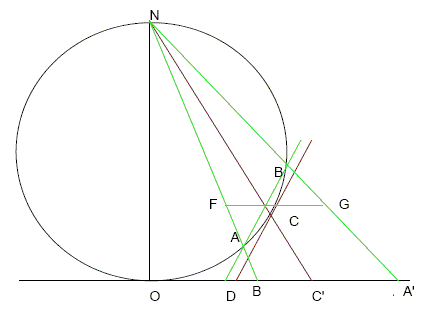
In the diagram, the point C is projected onto the point C' following the line from N and the line of intersection of the tangent plane and the xy-plane is the line orthogonal to the diagram through the point D.
To prove a) consider two planes that intersect in the line NC'. They intersect the tangent plane at C in lines defining an angle and they intersect the xy-plane in lines defining its image. Planes containing the common line of the tangent plane and the xy-plane intersect the planes defining the angle in angles that are maximum when it is orthogonal to CC' and decrease symmetrically as they go on either side of this plane. Since
| ∠DC'C = 90° - ∠ONC = ∠NOC' = ∠DC'C, |
the angles at C and C' will be equal as required. (Note in passing that, in general, stereographic projection does not preserves lengths and areas.)
Circles on the sphere are intersections of planes with the sphere. If the circle passes through N so does the plane it is in, and then its projection is the line of intersection of the plane with the xy-plane and any line in the xy-plane can be joined to N by a plane whose intersection with the sphere is a circle through N, which proves b).
For c) suppose that C is the centre of a circle on the sphere and A and B are the points where the circle meets the diagram so A' and B' are where its image meets the diagram. Since the arcs AC and BC are equal, the plane of the circle is parallel to the tangent plane at C and AB makes the same angle with NC' as the xy-plane does. If E is the intersection of NC and AB, the plane through E parallel to the xy-plane meets the elliptic cone joining N to the circle in a conic section passing through F and G. FG makes the same angle with NC' as AB does so EA = EG and EB = EF and the conic section is a circle the same size as the one on the sphere. The section of the cone by the xy-plane is obviously similar and is therefore a circle. Conversely, given a circle in the xy-plane, the argument can be reversed showing that its inverse image is a circle on the sphere.
Radical Axes
For two circles in the plane, the radical axis is defined to be the line of their intersection. Oddly enough, this definition works even when they do not have real points of intersection: the imaginary points of intersection lie on a real line. To show this, consider the equation of the circle S in standard form
| x² + y² + L(S) = 0, |
where L(S) = ax + by + c, a linear form. The points of intersection of two circles S1 and S2 are on the real line
| L(S1) - L(S2) = 0 |
which is therefore the equation of the radical axis of the two circles.
Note that, for three circles S1, S2 and S3, the radical axes meet in a point because
| L(S1) - L(S2) + L(S2) - L(S3) + L(S3) - L(S1) |
is identically zero.
Stereographic projection provides an alternative, purely geometrical, definition of the radical axis that works even for two non-intersecting circles: their inverse images on the sphere lie in planes that intersect in a line whose projection from N onto the plane is the radical axis. To check that it agrees with the common definition, it is sufficient to note that any circle that intersects both circles in real points defines a new plane in the 3-dimensional configuration and the common point of the radical axes is the projection of the intersection of the three planes and is therefore on the radical axis of the first two.
Also, it is easy to show that the radical axis of two circles S1 and S2 is orthogonal to the line joining their centers. Since
Note: Stereographic projection serves an enlightening model for another geometric construct, inversion - reflection in circle.
2D Problems That Benefit from a 3D Outlook
- Four Travellers, Solution
- Desargues' Theorem
- Soddy Circles and Eppstein's Points
- Symmetries in a Triangle
- Three Circles and Common Chords
- Three Circles and Common Tangents
- Three Equal Circles
- Menelaus from 3D
- Stereographic Projection and Inversion
- Stereographic Projection and Radical Axes
- Sum of Squares in Equilateral Triangle
Stereographic Projection
- Stereographic Projection and Radical Axes
- Stereographic Projection and Inversion
- Stereographic Projection of a Coffin Problem
- Stereographic Projection - an Interactive Tool
- Objects distant and near
Radical Axis and Radical Center
- How to Construct a Radical Axis
- A Property of the Line IO: A Proof From The Book
- Cherchez le quadrilatere cyclique II
- Circles On Cevians
- Circles And Parallels
- Circles through the Orthocenter
- Coaxal Circles Theorem
- Isosceles on the Sides of a Triangle
- Properties of the Circle of Similitude
- Six Concyclic Points
- Radical Axis and Center, an Application
- Radical axis of two circles
- Radical Axis of Circles Inscribed in a Circular Segment
- Radical Center
- Radical center of three circles
- Steiner's porism
- Stereographic Projection and Inversion
- Stereographic Projection and Radical Axes
- Tangent as a Radical Axis
- Two Circles on a Side of a Triangle
- Pinning Butterfly on Radical Axes
- Two Lines - Two Circles
- Two Triples of Concurrent Circles
- Circle Centers on Radical Axes
- Collinearity with the Orthocenter
- Six Circles with Concurrent Pairwise Radical Axes
- Six Concyclic Points on Sides of a Triangle
- Line Through a Center of Similarity
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73607167
