Butterflies in Quadrilaterals and Elsewhere

The Butterfly Theorem is one of the most popular and appealing in plane geometry. It has several variants and a few curious generalizations. Until very recently, all the known varieties of plane Butterflies were found in circles and their combinations. Then a new variety that inhabits quadrilaterals has been discovered. But, as Eisso Atzema, the author of the subsequent research put it, the later variety is the old one in disguise. The investigation has been supported by Desargues' Involution Theorem, see, for example [Dörrie, pp. 265-273]:

The points of intersection of a line with the three pairs of opposite sides of a complete quadrilateral and a conic section circumscribed about the quadrilateral form four pairs of an involution. The lines joining a point with the three pairs of opposite vertices of a complete quadrangle and the tangents drwan fom the point to a conic section inscribed into the quadrangle form four ray pairs of an involution.

Among other sources, see for example [Pedoe's Geometry or Coxeter's Projective Geometry]. The involution theorem will be discussed elsewhere. The report on the investiguation appears below practically verbatim.

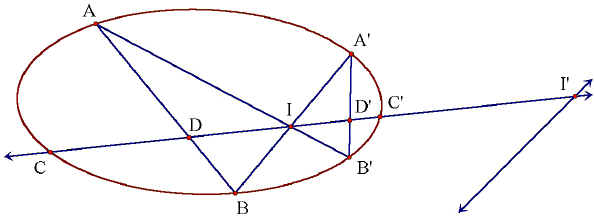
Here we reformulate the Butterfly Theorem in terms of projective geometry. Consider a self-intersecting quadrilateral AB'A'B (the "butterfly") inscribed in a conic section Γ. Let I be the point of intersection of the sides A'B and AB'. Now draw an arbitrary line through I and let C, C' be the points of intersection of the line with the conic section. By Desargues' Involution Theorem, the family of conic sections circumscribing AB'A'B defines an involution on the line CC', with I a fixed point of this involution and C, C' a conjugate pair (i.e. they are each other's images under the involution.) This completely determines the involution: Since the fixed points of an involution are in harmonic position with respect to any conjugate pair of points, we can determine the second fixed point I'. In fact, I' is the point of intersection of CC' with the polar line of I with respect to the conic section Γ. The involution on CC' is the circular inversion with respect to the circle that has II' for a diameter. It is easily verified that for this inversion one has for all conjugate points P, P' the equality

1/IP + 1/IP' = 2/II',

where the quantities IP, IP' and II' are directed distances.

Since C and C' form a conjugate pair while D = AB∩CC', D' = A'B'∩CC' form another one, it follows that

1/IC + 1/IC' = 1/ID + 1/ID',

with a reference to the above diagram,

1/|IC| - 1/|IC'| = 1/|ID| - 1/|ID'|,

where |.| denotes the "absolute" common distance between two points. This is a generalization of Candy's version of the Butterfly Theorem.

The connection between the two families of butterflies is illustrated below:

For a (convex) quadrilateral ABCD, let I be the point of intersection of the diagonals AC and BD. For any line passing through I, let G and G' the points of intersection with DA and CB, respectively. Now consider the family of conic sections passing through D, B, G and G'. Since five points determine a conic section, there is a unique conic section CH in this family that passes through a given point H on AB. Next draw the line HI. Let H' be the point of intersection of HI with DC and let H_o be the second point of intersection of HI with CH. The point H_o will be the image of the point H under the involution on HI defined by the family of conic sections through D, B, G and G'. But this involution has I for a fixed point and the points H'' = HI∩CB and H''' = HI∩AD for a conjugate pair. This uniquely determines the involution. However, under the involution induced on HI by the family of conic sections circumscribing ABCD the same points H'' and H''' form a conjugate pair as well, while I again is a fixed point. In other words, the two families of conic sections give rise to the same involution on HI. According to this second definition of the involution, the image of H is H'. It follows that H' and H_o coincide. Consequently D, B, G, G', H and H' all lie on the same conic. Alternatively, if we wanted to use a slightly more heavy-duty tool of projective geometry, we could have noted that GD∩HB = A, DH'∩BG' = C, and H'H∩G'G = I are collinear. Therefore, by the converse of Pascal's Theorem, it follows that there is a conic that circumscribes the (self-intersecting) hexagon GDH'HBG'. Either way, this means that we have the set-up of the Butterfly Theorem as outlined at the beginning. Kung's Theorem immediately follows.

It's the same butterfly ... under a different light.

References

E. J. Atzema, Butterflies in Quadrilaterals: A Comment on a Note by Sidney Kung, Math Magazine 80, n 1 (Feb. 2007), pp. 70-72
H. S. M. Coxeter, Projective Geometry, Springer; 2 edition (October 9, 2003)
H. Dörrie, 100 Great Problems Of Elementary Mathematics, Dover Publications, NY, 1965
D. Pedoe, Geometry: A Comprehensive Course, Dover, 1970

Butterfly Theorem and Variants

71868001