Butterfly in Inscriptible Quadrilateral

Here's a problem by Dao Thanh Oai with a solution by Telv Cohl.

Let $ABC$ be an inscriptible quadrilateral with the incircle $(O),$ $E=AC \cap BD.$ Let a line through $E$ meets $AD,$ $BC$ in $F$ and $G,$ respectively. Assume also, it meets $(O)$ at $H$ and $I,$ as in the diagram.

Butterfly in Inscriptible Quadrilateral- problem

Prove that $EI=EH$ iff $EF=EG.$

Proof

If $(O)$ touches $AD,$ $BC$ at $X,$ $Y,$ respectively, then, as is well known, $X,$ $E,$ $Y$ are collinear. Desargues' Involution Theorem applied to the degenerate quadrangle $XXYY,$ informs us that $E$ is a double fixed point of the involution defined on the given line, with $F,G$ and $H,I$ reciprocal pairs.

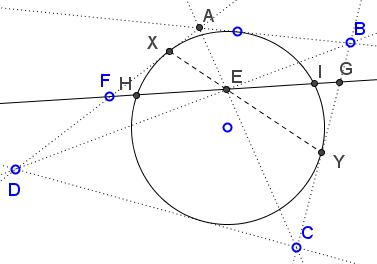
Butterfly in Inscriptible Quadrilateral- solution

The condition $EI=EH$ means that the involution is a symmetry in $E,$ implying $EF=EG.$

Note: the proof above is reminiscent of Hubert Shutrick's proof (Proof #20) of the common Butterfly Theorem.

Reference

  1. Michael Woltermann, Desargues’ Involution Theorem

Butterfly Theorem and Variants

  1. Butterfly theorem
  2. 2N-Wing Butterfly Theorem
  3. Better Butterfly Theorem
  4. Butterflies in Ellipse
  5. Butterflies in Hyperbola
  6. Butterflies in Quadrilaterals and Elsewhere
  7. Pinning Butterfly on Radical Axes
  8. Shearing Butterflies in Quadrilaterals
  9. The Plain Butterfly Theorem
  10. Two Butterflies Theorem
  11. Two Butterflies Theorem II
  12. Two Butterflies Theorem III
  13. Algebraic proof of the theorem of butterflies in quadrilaterals
  14. William Wallace's Proof of the Butterfly Theorem
  15. Butterfly theorem, a Projective Proof
  16. Areal Butterflies
  17. Butterflies in Similar Co-axial Conics
  18. Butterfly Trigonometry
  19. Butterfly in Kite
  20. Butterfly with Menelaus
  21. William Wallace's 1803 Statement of the Butterfly Theorem
  22. Butterfly in Inscriptible Quadrilateral
  23. Camouflaged Butterfly
  24. General Butterfly in Pictures
  25. Butterfly via Ceva
  26. Butterfly via the Scale Factor of the Wings
  27. Butterfly by Midline
  28. Stathis Koutras' Butterfly
  29. The Lepidoptera of the Circles
  30. The Lepidoptera of the Quadrilateral
  31. The Lepidoptera of the Quadrilateral II
  32. The Lepidoptera of the Triangle
  33. Two Butterflies Theorem as a Porism of Cyclic Quadrilaterals
  34. Two Butterfly Theorems by Sidney Kung
  35. Butterfly in Complex Numbers

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

70787829