Stathis Koutras' Butterfly
What Is This About?
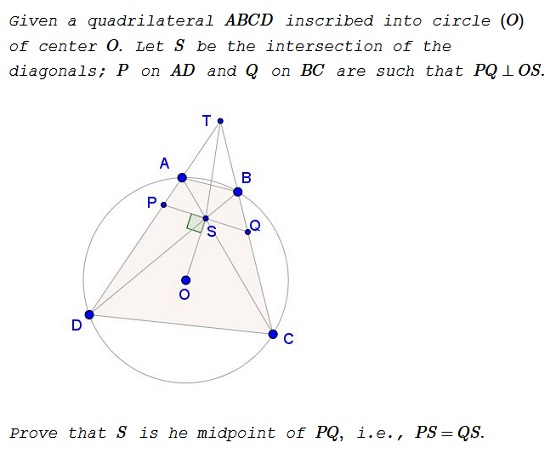
Problem
Solution
Let $EM,FN\,$ be the orthogonal projections of $SO\,$ on $AD,BC,\,$ respectively. And let $T\,$ be the intersection of $AD\,$ and $BC.\,$
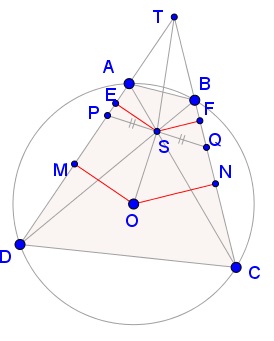
(1)
$\displaystyle\frac{EM}{FN}=\frac{TQ}{TP}.$
But $EM,FN\,$ are the corresponding segments of obviously similar triangles $SAD\,$ and $SBC\,$ ($E,F\,$ are the feet of the altitudes whereas $M,N\,$ the midpoints of the corresponding sides) and, therefore, their ratio shall be equal to the ratio of the corresponding altitudes, i.e., $\displaystyle\frac{EM}{FN}=\frac{SE}{SF}.\,$ Combining this with (1),
$\displaystyle\frac{TQ}{TP}=\frac{SE}{SF}\,\Rightarrow\,TQ\cdot SF=TP\cdot SE\,\Rightarrow\,[\Delta TSQ]=[\Delta TSP],$
where $[X]\,$ denotes the area of shape $X.\,$ The two triangles share the altitude from $T,\,$ implying that $S\,$ is indeed the midpoint of $PQ,\,$ thus proving the Butterfly Theorem.
Acknowledgment
Stathis Koutras has kindly posted at the CutTheKnotMath facebook page his novel proof of the Butterfly Theorem.
Butterfly Theorem and Variants
- Butterfly theorem
- 2N-Wing Butterfly Theorem
- Better Butterfly Theorem
- Butterflies in Ellipse
- Butterflies in Hyperbola
- Butterflies in Quadrilaterals and Elsewhere
- Pinning Butterfly on Radical Axes
- Shearing Butterflies in Quadrilaterals
- The Plain Butterfly Theorem
- Two Butterflies Theorem
- Two Butterflies Theorem II
- Two Butterflies Theorem III
- Algebraic proof of the theorem of butterflies in quadrilaterals
- William Wallace's Proof of the Butterfly Theorem
- Butterfly theorem, a Projective Proof
- Areal Butterflies
- Butterflies in Similar Co-axial Conics
- Butterfly Trigonometry
- Butterfly in Kite
- Butterfly with Menelaus
- William Wallace's 1803 Statement of the Butterfly Theorem
- Butterfly in Inscriptible Quadrilateral
- Camouflaged Butterfly
- General Butterfly in Pictures
- Butterfly via Ceva
- Butterfly via the Scale Factor of the Wings
- Butterfly by Midline
- Stathis Koutras' Butterfly
- The Lepidoptera of the Circles
- The Lepidoptera of the Quadrilateral
- The Lepidoptera of the Quadrilateral II
- The Lepidoptera of the Triangle
- Two Butterflies Theorem as a Porism of Cyclic Quadrilaterals
- Two Butterfly Theorems by Sidney Kung
- Butterfly in Complex Numbers
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73573068
