Circles through the Orthocenter

The applet below illustrates Problem 1 from the 2008 International Mathematics Olympiad:

An acute-angled triangle $ABC\;$ has orthocentre $H.\;$ The circle passing through $H\;$ with centre the midpoint of $BC\;$ intersects the line $BC\;$ at $A_{1}\;$ and $A_{2}.\;$ Similarly, the circle passing through $H\;$ with centre the midpoint of $CA\;$ intersects the line $CA\;$ at $B_{1}\;$ and $B_{2},\;$ and the circle passing through $H\;$ with centre the midpoint of $AB\;$ intersects the line $AB\;$ at $C_{1}\;$ and $C_{2}.\;$ Show that $A_{1},\;$ $A_{2},\;$ $B_{1},\;$ $B_{2},\;$ $C_{1},\;$ $C_{2}\;$ lie on a circle.

6 April 2016, Created with GeoGebra

Solution

Solution 1

One solution stems from the observation that the orthocenter serves as the radical center of the three circles whilst the altitudes are the radical axes of the circles taken in pairs. The situation is reminscent of the circles constructed on the sides of a triangle as diameters.

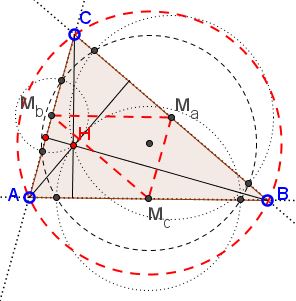
circles through the orthocenter

Consider the circles centered at the midpoints $M_{a}\;$ and $M_{b}\;$ of sides $BC\;$ and $AC,\;$ respectively. Since $CH\perp AB\;$ we also have $M_{a}M_{b}\perp CH.\;$ But the line joining the centers of two intersecting circles is perpendicular to their common chord. In particular, this is what $CH\;$ is - the line containing the common chord of the two circles. Which exactly means that $CH\;$ is their radical axis.

The same holds for the other two pairs of circles.

Let $r_{a},\;$ $r_{b},\;$ $r_{c}\;$ be the radii of the circles centered at $M_{a},\;$ $M_{b},\;$ $M_{c},\;$ which we denote $C(M_{a}, r_{a}),\;$ $C(M_{b}, r_{b}),\;$ $C(M_{c}, r_{c}),\;$ respectively. Let also set $a = BC,$ $b = AC,$ $c = AB.$

Since $C\;$ lies on the radical axis of $C(M_{a}, r_{a})\;$ and $C(M_{b}, r_{b}),\;$ we may apply the Pythagorean theorem to the triangles formed by tangents of common length $t\;$ from $C\;$ to the two circles, half-sides of $BC\;$ and $AC\;$ and the radii of the circles:

(1)

$(a/2)^{2} - r_{a}^{2} = t^{2} = (b/2)^{2} - r_{b}^{2}.\;$

On the other hand, if the six points $A_{1},\;$ $A_{2},\;$ $B_{1},\;$ $B_{2},\;$ $C_{1},\;$ $C_{2}\;$ lie on a circle, the latter is bound to be centered at the circumcenter O of $\Delta ABC.\;$ So lets show that $O\;$ is equidistant from the six points. To this end, denote $s_{a} = OM_{a},$ $s_{b} = OM_{b},$ $s_{c} = OM_{c}.$ Since, $O\;$ is the circumcenter of $\Delta ABC,\;$

(2)

$(a/2)^{2} + s_{a}^{2} = R^{2} = (b/2)^{2} + s_{b}^{2},\;$

$R\;$ being the circumradius of $\Delta ABC.\;$ Subtracting (1) from (2) we see that

(3)

$r_{a}^{2} + s_{a}^{2} = r_{b}^{2} + s_{b}^{2},\;$

implying that $O\;$ is equidistant from $A_{1},\;$ $A_{2},\;$ $B_{1},\;$ $B_{2}.\;$ The four points $A_{1},\;$ $A_{2},\;$ $B_{1},\;$ $B_{2}\;$ are thus concyclic. Similarly, $A_{1},\;$ $A_{2},\;$ $C_{1},\;$ $C_{2}\;$ are equidistant from $O\;$ which puts $C_{1}\;$ and $C_{2}\;$ on the same circle.

Observe now that the requirement for $\Delta ABC\;$ to be acute is spurious. The six points $A_{1},\;$ $A_{2},\;$ $B_{1},\;$ $B_{2},\;$ $C_{1},\;$ $C_{2}\;$ are concyclic for any $\Delta ABC.\;$ A further generalization replaces the altitudes with arbitrary concurrent cevians. Which shows that both requirements are nothig but red herrings.

Solution 2

This solution is by Jack D'Aurizio.

We may put a reference system with its centre at the circumcentre of $\Delta ABC,\;$ so that, by Euler's theorem, we simply have $H=A+B+C.\;$ We have to show $CA_1\cdot CA_2 = CB_1\cdot CB_2\;$ and so on, but: $CA_1\cdot CA_2 = \frac{1}{4}\|B-C\|^2 -\frac{1}{4}\|B+C+2A\|^2,\;$ hence the problem boils down to proving:

$ \|B+C\|^2 - \|B+C+2A\|^2 = \|A-C\|^2 - \|A+C+2B\|^2. $

That is straightforward, since both the LHS and the RHS equal:

$\begin{eqnarray*} && -4R^2\left(1+\cos(2A)+\cos(2B)+\cos(2C)\right)\\&=&-4R^2\left(4-2\sin^2 A-2\sin^2 B-2\sin^2 C\right)\\&=&2(a^2+b^2+c^2)-16R^2=2(R^2-OH^2).\end{eqnarray*}$

What Is Red Herring

Radical Axis and Radical Center

71862915