The Lepidoptera of the Quadrilateral
The Butterfly Theorem is one of the most popular and appealing in plane geometry. It has several variants and a few curious generalizations. Until very recently, all the known varieties of plane Butterflies were found in circles and their combinations. But no longer. A new variety that inhabits quadrilaterals has been just discovered. We can compare the typical species side by side:

The closest to the newly discovered is that described by Steve Conrad: Through a point I on a chord AC of a circle, two other chords EF and HG are drawn. If EG and HF intersect AC in M and N, respectively, then
1/IM - 1/IA = 1/IN - 1/IC.
If we introduce a = IA, m = IM, c = IC, n = IN, then the above will appear as
| (1) | 1/m - 1/a = 1/n - 1/c. |
The new variety has been described by S. Kung:
Theorem
Through the intersection I of the diagonals AC, BD of a convex quadrilateral ABCD, draw two lines EF and HG that meet the sides of ABCD in E, F, G, H. Let M and N be the intersections of EG and FH with AC. Then (1) holds.
The proof of the theorem is based on two simple lemmas.
Lemma 1
If K is the intersection of segments XY and UV, V distinct from K, then
Area( Δ UXY)/Area( Δ VXY) = UK/VK.
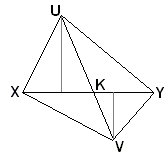
This is true because the two triangles share a base. Their areas therefore are in the ratio of their altitudes. The latter, along with XY and UV, cut two similar right triangles, in which the ratio of the corresponding sides is UK/VK.
Lemma 2
Given triangles ABC and XYZ such that either ∠ABC = ∠XYZ or

Area( Δ ABC)/Area( Δ XYZ) = AB/XY·BC/YZ.
The proof is similar to that of Lemma 1.
Proof of Theorem
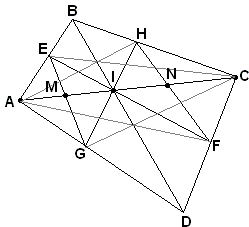
There are 12 pairs of triangles to which we may apply either Lemma 1 or Lemma 2. We get successively
| AM/IM | = Area( Δ AEG)/Area( Δ IEG) |
| IN/CN | = Area( Δ IHF)/Area( Δ CHF) |
| IC/IA | = Area( Δ CBD)/Area( Δ ABD) |
| IE/IF·IG/IH | = Area( Δ IEG)/Area( Δ IHF) |
| CH/BC·CF/CD | = Area( Δ CHF)/Area( Δ CBD) |
| AB/AE·AD/AG | = Area( Δ ABD)/Area( Δ AEG) |
| IF/IE | = Area( Δ AFC)/Area( Δ AEC) |
| IH/IG | = Area( Δ AHC)/Area( Δ AGC) |
| CD/CF | = Area( Δ CAD)/Area( Δ AFC) |
| BC/CH | = Area( Δ ABC)/Area( Δ AHC) |
| AE/AB | = Area( Δ AEC)/Area( Δ ABC) |
| AG/AD | = Area( Δ AGC)/Area( Δ CAD) |
Multiplying all twelve yields
AM/IM·IN/CN·IC/IA = 1,
or
(a - m)/m·n/(c - n)·c/a = 1.
Rewriting this once more we obtain
(a - m)/(am) = (c - n)/(cn),
which is the same as (1).
We should note that the new variety of butterflies admits generalizations similar to their circular relatives. For example, based on the same consideration we can claim the existence of 2N-winged butterflies dwelling on (co-diagonal) rectangles.
References
Butterfly Theorem and Variants
- Butterfly theorem
- 2N-Wing Butterfly Theorem
- Better Butterfly Theorem
- Butterflies in Ellipse
- Butterflies in Hyperbola
- Butterflies in Quadrilaterals and Elsewhere
- Pinning Butterfly on Radical Axes
- Shearing Butterflies in Quadrilaterals
- The Plain Butterfly Theorem
- Two Butterflies Theorem
- Two Butterflies Theorem II
- Two Butterflies Theorem III
- Algebraic proof of the theorem of butterflies in quadrilaterals
- William Wallace's Proof of the Butterfly Theorem
- Butterfly theorem, a Projective Proof
- Areal Butterflies
- Butterflies in Similar Co-axial Conics
- Butterfly Trigonometry
- Butterfly in Kite
- Butterfly with Menelaus
- William Wallace's 1803 Statement of the Butterfly Theorem
- Butterfly in Inscriptible Quadrilateral
- Camouflaged Butterfly
- General Butterfly in Pictures
- Butterfly via Ceva
- Butterfly via the Scale Factor of the Wings
- Butterfly by Midline
- Stathis Koutras' Butterfly
- The Lepidoptera of the Circles
- The Lepidoptera of the Quadrilateral
- The Lepidoptera of the Quadrilateral II
- The Lepidoptera of the Triangle
- Two Butterflies Theorem as a Porism of Cyclic Quadrilaterals
- Two Butterfly Theorems by Sidney Kung
- Butterfly in Complex Numbers
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73598989
