Line Through a Center of Similarity
What is this about?
Problem
$P$ is a center of similarity of circles $(O_{1})$ and $(O_{2}),$ centered at $O_{1}$ and $O_{2},$ respectively. A line through $P$ meets $(O_{i})$ at points $A_{i}$ and $B_{i},$ $i=1,2.$ The tangents to the circles, one at $A_{1},$ the other at $B_{2},$ meet at $X,$ those at $A_{2}$ and $B_{1}$ meet at $Y.$
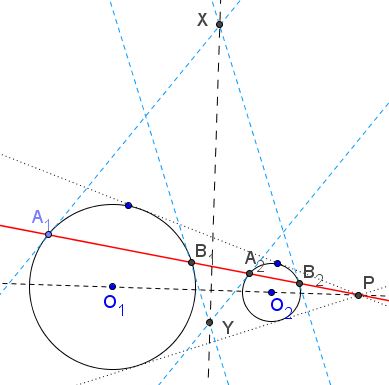
Prove that $XY$ is the radical axis of the two circles.
Solution
Since the given line passes through a center of similarity of the two circles, $A_{1},$ say, maps on $A_{2}$ and $B_{1}$ on $B_{2}.$ Naturally, $O_{1}$ maps on $O_{2}.$
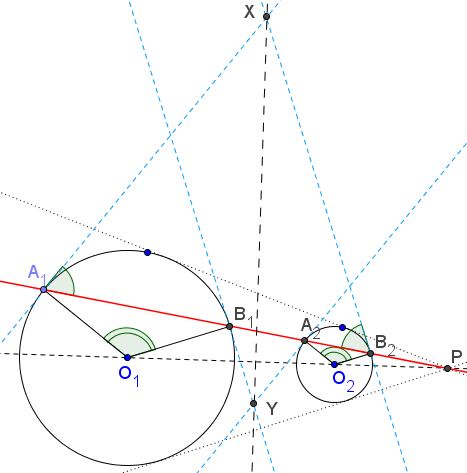
This, in particular, means that $\angle A_{1}O_{1}B_{1}=\angle A_{2}O_{2}B_{2}$ and that the pairs of the tangents are parallel: $A_{1}X\parallel A_{2}Y$ and $B_{2}X\parallel B_{1}Y.$ The angle between a chord and a tangent at one of the chord's endpoints equals half the central angle subtended by the chord. Thus, $\angle A_{1}B_{2}X=\angle B_{2}A_{1}X,$ implying $A_{1}X=B_{2}X.$ Similarly, $A_{2}Y=B_{1}Y,$ which exactly means that both $X$ and $Y$ lie on the radical axis of the to circles.
The diagram above illustrates the case of the external center of similarity. The case of the internal center is entirely similar.
Note: The case where the given line does not pass through one of the centers of similarity is treated on a separate page.
Acknowledgment
This is problem 251a from the second volume of I. M. Yaglom's Geometric Transformations, Russian edition (1956.) I am pretty sure that the problem has been included in the fourth volume of the English translation, but not owning the book I am unable to verify that fact.
Radical Axis and Radical Center
- How to Construct a Radical Axis
- A Property of the Line IO: A Proof From The Book
- Cherchez le quadrilatere cyclique II
- Circles On Cevians
- Circles And Parallels
- Circles through the Orthocenter
- Coaxal Circles Theorem
- Isosceles on the Sides of a Triangle
- Properties of the Circle of Similitude
- Six Concyclic Points
- Radical Axis and Center, an Application
- Radical axis of two circles
- Radical Axis of Circles Inscribed in a Circular Segment
- Radical Center
- Radical center of three circles
- Steiner's porism
- Stereographic Projection and Inversion
- Stereographic Projection and Radical Axes
- Tangent as a Radical Axis
- Two Circles on a Side of a Triangle
- Pinning Butterfly on Radical Axes
- Two Lines - Two Circles
- Two Triples of Concurrent Circles
- Circle Centers on Radical Axes
- Collinearity with the Orthocenter
- Six Circles with Concurrent Pairwise Radical Axes
- Six Concyclic Points on Sides of a Triangle
- Line Through a Center of Similarity
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73606510
