A Proof of the Butterfly Theorem Using Ceva’s Theorem
Cesare Donolato
Forum Geometricorum, Volume 16 (2016) 185–186
Theorem (The Butterfly Theorem)
Through the midpoint $M\;$ of a chord $PQ\;$ of a circle, two other chords $AB\;$ and $CD\;$ are drawn. Chords $AD\;$ and $BC\;$ intersect $PQ\;$ at points $X\;$ and $Y,\;$ respectively.
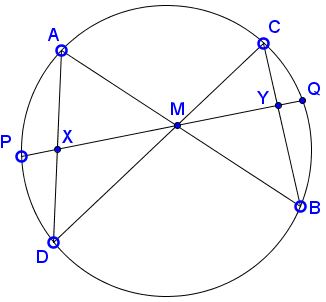
Then $M\;$ is also the midpoint of $XY.$
We introduce the points $A'\;$ and $D'\,$ that are the symmetric of $A\;$ and $D\;$ about $M,\;$ respectively. Hence, $MA' = MA\;$ and $MD' = MD.\;$ Next we connect the point $D'\;$ to $A'\;$ and $B,\;$ and call $E\;$ the intersection of $DB\;$ with the line through $P\;$ and $Q.\;$ Thus we have constructed triangle $MBD'\;$ with cevians $D'A',\;$ $ME,\;$ and $BC.\;$

We show that the segment $DA\;$ cuts the chord $PQ\;$ at the same point $Y\;$ as $BC,\;$ i.e., that the three cevians are concurrent at $Y.\;$ This property will be proved by applying Ceva’s theorem to triangle $MBD'.\;$
Lemma
In triangle $MBD,\;$ the cevians $DA,\;$ $ME,\;$ and $BC\;$ are concurrent at $Y.\;$
Proof of Lemma
We set $MA'=MA=\rho_1,\;$ $MB=r_1,\;$ $MC=r_2\;$ and $MD'=MD=\rho_2.\;$ We observe that $\displaystyle\frac{BE}{ED'}=\frac{r_1\sin\beta}{\rho_2\sin\alpha},\;$ the ratio of respective distances of $B\;$ and $D'\;$ from the line $PQ.\;$ Moreover, $A'B=r_1-\rho_1,\;$ and $D'C=\rho_2-r_2.\;$ Now,
(1)
$\displaystyle\begin{align} \frac{BE}{ED'}\cdot\frac{D'C}{CM}\cdot\frac{MA'}{A'B} &= \frac{r_1\sin\beta}{\rho_2\sin\alpha}\cdot\frac{\rho_2-r_2}{r_2}\cdot\frac{\rho_1}{r_1-\rho_1}\\ &=\frac{(\rho_2-r_2)\sin\beta}{(r_1-\rho_1)\sin\alpha}, \end{align}$
since $\rho_1r_1=\rho_2r_2\;$ by the Intersecting Chords Theorem.
The differences appearing in (1) can be written in terms of the distance $d = OM\;$ of the circle center $O\;$ to the chord $PQ,\;$ and the angles $\alpha\;$ and $\beta.\;$ The above figure shows that the projection of $OM\;$ onto the chord $PQ\;$ has length $d\sin\alpha,\;$ so that we get $\displaystyle\rho_2=\frac{1}{2}CD+d\sin\alpha,\;$ and $\displaystyle r_2=\frac{1}{2}C-d\sin\alpha.\;$ Hence, $\rho_2-r_2=2d\sin\alpha.\;$ Similarly, we find $r_1-\rho_1=2d\sin\beta.$ Substituting these expressions into (1) we obtain
$\displaystyle\frac{BE}{ED'}\cdot\frac{D'C}{CM}\cdot\frac{MA'}{A'B}=1.$
By Ceva's Theorem, the cevians $D'A',\;$ $ME,\;$ and $BC\;$ are concurrent. The common point is clearly $Y.$
Proof of Butterfly Theorem
We observe that triangle $MA'D'\;$ is congruent by construction to triangle $MAD,\;$ because two sides of the first $(MA',MD')\;$ are equal to two sides of the second $(MA,MD),\;$ and the included angles are equal. It follows that $\angle MD'Y = \angle MDX.\;$ Consequently, triangles $MD'Y\;$ and $MDX\;$ are also congruent, since they have equal two pairs of angles $(\angle MD'Y = \angle MDX,\;$ and $\angle YMD'= \angle XMD,\;$ vertical angles), as well as the included sides $(MD' = MD).\;$ This congruence implies that the corresponding sides $MY\;$ and $MX\;$ are equal. Therefore, $M\;$ is the midpoint of $XY\;$ and the butterfly theorem is proved.
Remark
It is rather interesting to compare this proof to William Wallace's 1803 Statement.
Butterfly Theorem and Variants
- Butterfly theorem
- 2N-Wing Butterfly Theorem
- Better Butterfly Theorem
- Butterflies in Ellipse
- Butterflies in Hyperbola
- Butterflies in Quadrilaterals and Elsewhere
- Pinning Butterfly on Radical Axes
- Shearing Butterflies in Quadrilaterals
- The Plain Butterfly Theorem
- Two Butterflies Theorem
- Two Butterflies Theorem II
- Two Butterflies Theorem III
- Algebraic proof of the theorem of butterflies in quadrilaterals
- William Wallace's Proof of the Butterfly Theorem
- Butterfly theorem, a Projective Proof
- Areal Butterflies
- Butterflies in Similar Co-axial Conics
- Butterfly Trigonometry
- Butterfly in Kite
- Butterfly with Menelaus
- William Wallace's 1803 Statement of the Butterfly Theorem
- Butterfly in Inscriptible Quadrilateral
- Camouflaged Butterfly
- General Butterfly in Pictures
- Butterfly via Ceva
- Butterfly via the Scale Factor of the Wings
- Butterfly by Midline
- Stathis Koutras' Butterfly
- The Lepidoptera of the Circles
- The Lepidoptera of the Quadrilateral
- The Lepidoptera of the Quadrilateral II
- The Lepidoptera of the Triangle
- Two Butterflies Theorem as a Porism of Cyclic Quadrilaterals
- Two Butterfly Theorems by Sidney Kung
- Butterfly in Complex Numbers
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73606509
