Butterflies in Hyperbola

Sidney H. Kung

We give an analytic proof of the Butterfly Theorem for hyperbolas.

Theorem

Let M(0, k) be the midpoint of a chord AB parallel to the major axis of a hyperbola. Through M two other chords CD and EF are drawn. ED cuts AB at P and CF cuts AB at Q. Then M is also the midpoint of PQ.

Proof

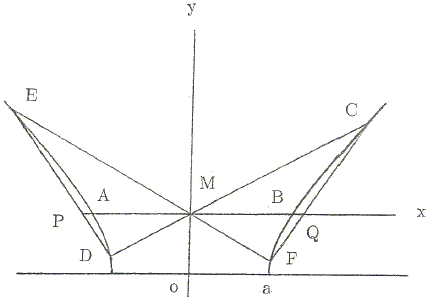
Through M, we introduce a new set of x-y-axes. Then the equation of the hyperbola is

(1)	x² a² - (y + k)² b² = 1

or,

(1')	b²x² - a²(y + k)² - a²b² = 0.

Assume that the coordinates of the related points are as follows: M(0, 0), C(x₁, y₁), D(x₂, y₂), E(x₃, y₃), F(x₄, y₄), P(p, 0), Q(q, 0); and that the equations of lines DC and EF are y = m₁x and y = m₂x, respectively.

Substituting m₁x into (1') gives

(2)	(b² - a²m1²) x² - 2a²m1kx - a² (b² + k²) = 0.

The roots, x₁ and x₂, of equation (2) are the x-coordinates of C and D, where

x1 + x2

=

- - 2m1ka² b² - m1²a²

    and    

x1	x2 = - a²(b² + k²) b² - m1²a²

Dividing these, we get

m1x1x2 x1 + x2

=

- (b² + k²) 2k

Similarly, by substituting y = m₂x into (2) we will get

m2x3x4 x3 + x4

=

- (b² + k²) 2k

also (x₃ and x₄ are x-coordinates of E and F). Thus,

(*)	m1x1x2 x1 + x2 = m2x3x4 x3 + x4

which can further be rearranged (see note (I) below) to become

(3)	- x2x3 m1x2 - m2x3 = x1x4 m1x1 - m2x4

Observe that C, Q, F are collinear. The slope of QC and that of FQ are equal. So,

y1 x1 - q

=

- y4 q - x4

Hence,

(4)	q - x1 q - x4 = y1 y4 = m1x1 m2x4

q ≠ x₁ and q ≠ x₄.

Solving (4) for q, we have

q

=

(m1 - m2) x1x4 m1x1 - m2x4

In a similar manner, by equating the slopes of PE and DP we can get

p

=

(m1 - m2) x2x3 m1x2 - m2x3

Now by comparing p and q, and taking into account (3), it is easy to see that |p| = |q|. Therefore, MP = MQ.

Note

1. Derivation of (3): cross-multiplying and rearranging,

   	m1x1x2(x3 + x4)	= m2x3x4(x1 + x2)
   	m1x1x2x3 - m2x3x2x4	= m2x3x4x1 - m1x1x2x4
   	x2x3(m1x1 - m2x4)	= x1x4(m2x3 - m1x2),

   implying (3).

2. The above results are valid for parabolas. To verify, one may use the equation x² = p(y + k), p, k > 0, to start.

Butterfly Theorem and Variants

1. Butterfly theorem
2. 2N-Wing Butterfly Theorem
3. Better Butterfly Theorem
4. Butterflies in Ellipse
5. Butterflies in Hyperbola
6. Butterflies in Quadrilaterals and Elsewhere
7. Pinning Butterfly on Radical Axes
8. Shearing Butterflies in Quadrilaterals
9. The Plain Butterfly Theorem
10. Two Butterflies Theorem
11. Two Butterflies Theorem II
12. Two Butterflies Theorem III
13. Algebraic proof of the theorem of butterflies in quadrilaterals
14. William Wallace's Proof of the Butterfly Theorem
15. Butterfly theorem, a Projective Proof
16. Areal Butterflies
17. Butterflies in Similar Co-axial Conics
18. Butterfly Trigonometry
19. Butterfly in Kite
20. Butterfly with Menelaus
21. William Wallace's 1803 Statement of the Butterfly Theorem
22. Butterfly in Inscriptible Quadrilateral
23. Camouflaged Butterfly
24. General Butterfly in Pictures
25. Butterfly via Ceva
26. Butterfly via the Scale Factor of the Wings
27. Butterfly by Midline
28. Stathis Koutras' Butterfly
29. The Lepidoptera of the Circles
30. The Lepidoptera of the Quadrilateral
31. The Lepidoptera of the Quadrilateral II
32. The Lepidoptera of the Triangle
33. Two Butterflies Theorem as a Porism of Cyclic Quadrilaterals
34. Two Butterfly Theorems by Sidney Kung
35. Butterfly in Complex Numbers

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny