Butterfly theorem, a Projective Proof

The Butterfly Theorem is an obvious corollary of the following statement. This observation and the proof that follows are due to Mikhail Goldenberg (The Ingenuity Project, Baltimore, MD) and Mark Kaplan (Towson State University)

Theorem

Let L be a nondegenerated second degree curve. Suppose, three lines in the plane of L concur at the point M. Let points A, B; P, Q; and C, D be the intersections of these lines with L, and let AD and BC intersect PQ at X and Y, respectively. Finally, let N be the point harmonic conjugate to M with respect to the pair of points (P, Q). Then N is harmonic conjugate to M with respect to the pair of points (X, Y). In short,

(P, Q; M, N) = -1 ⇒ (X, Y; M, N) = -1.

a projective proof of the butterfly theorem

Proof

First, note that if a rectangle can be inscribed in a nondegenerated second degree curve, then the curve is a central one and its center coincides with the center of the rectangle. Second, the projective transformation preserves the cross ratio. Therefore, it is sufficient to prove the theorem for some projective image of the given configuration.

There exists a projective transformation of the plane of L which maps the quadrilateral ACBD onto a square A'C'B'D'. The image M' of the point M is the center of the square which is, as observed, the center of the image L' of the curve L. Therefore, M' is the midpoint of both segments, P'Q' and X'Y' , and the point N' is at infinity on the line P'Q' because (P, Q; M, N) = -1. So, N' is the harmonic conjugate point for M' with respect to (X', Y').

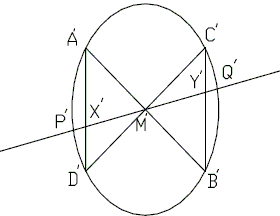
a projective proof of the butterfly theorem, second diagram

This completes the proof.

Butterfly Theorem and Variants

  1. Butterfly theorem
  2. 2N-Wing Butterfly Theorem
  3. Better Butterfly Theorem
  4. Butterflies in Ellipse
  5. Butterflies in Hyperbola
  6. Butterflies in Quadrilaterals and Elsewhere
  7. Pinning Butterfly on Radical Axes
  8. Shearing Butterflies in Quadrilaterals
  9. The Plain Butterfly Theorem
  10. Two Butterflies Theorem
  11. Two Butterflies Theorem II
  12. Two Butterflies Theorem III
  13. Algebraic proof of the theorem of butterflies in quadrilaterals
  14. William Wallace's Proof of the Butterfly Theorem
  15. Butterfly theorem, a Projective Proof
  16. Areal Butterflies
  17. Butterflies in Similar Co-axial Conics
  18. Butterfly Trigonometry
  19. Butterfly in Kite
  20. Butterfly with Menelaus
  21. William Wallace's 1803 Statement of the Butterfly Theorem
  22. Butterfly in Inscriptible Quadrilateral
  23. Camouflaged Butterfly
  24. General Butterfly in Pictures
  25. Butterfly via Ceva
  26. Butterfly via the Scale Factor of the Wings
  27. Butterfly by Midline
  28. Stathis Koutras' Butterfly
  29. The Lepidoptera of the Circles
  30. The Lepidoptera of the Quadrilateral
  31. The Lepidoptera of the Quadrilateral II
  32. The Lepidoptera of the Triangle
  33. Two Butterflies Theorem as a Porism of Cyclic Quadrilaterals
  34. Two Butterfly Theorems by Sidney Kung
  35. Butterfly in Complex Numbers

|Contact| |Front page| |Contents| |Geometry| |Butterfly theorem|

Copyright © 1996-2018 Alexander Bogomolny

71866563