Butterfly with Menelaus

Sidney Kung
September 7, 2012

We give a proof of the following by using Menelaus' theorem:

Through a point \(P\) of the line segment \(AB\) whose end points \(A\) and \(B\) lie on two intersecting lines \(l\) and \(l'\), respectively, draw \(CD\) and \(EF\) \((C, F\in l\), and \(E,D\in l')\). Let \(CE\cap AB=X\), \(FD\cap AB=Y.\space\)Then \(PA = PB\) implies \(PX = PY.\)

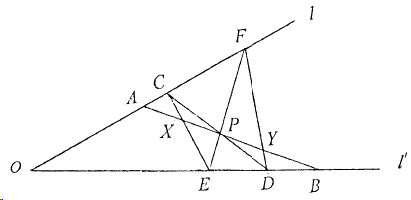
statement of the butterfly theorem in a quadrilateral

Proof

For a repeated application of Menelaus' here, we shall proceed by focusing on parts of the diagram:

  1. \(\triangle OFE\) cut by transversal \(CPD\)

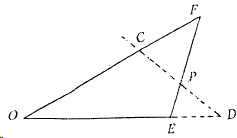
    first step of the proof

    \(\frac{OC}{CF}\times \frac{FP}{PE}\times \frac{ED}{DO} = 1\).

  2. \(\triangle OAB\) cut by transversal \(CPD\)

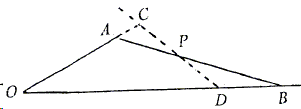
    second step of the proof

    \(\frac{OD}{DB}\times \frac{BP}{PA}\times \frac{AC}{CO} = 1\).

  3. \(\triangle PBE\) cut by transversal \(FYD\)

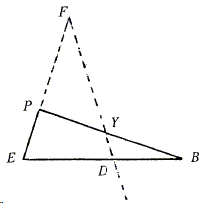
    third step of the proof

    \(\frac{PY}{YB}\times \frac{BD}{DE}\times \frac{EF}{FP} = 1\).

  4. \(\triangle FAP\) cut by transversal \(CXE\)

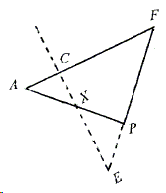
    fourth step of the proof

    \(\frac{PE}{EF}\times \frac{FC}{CA}\times \frac{AX}{XP} = 1\).

Multiplying the four identities and simplifying gives \(\frac{PY}{YB}\times \frac{AX}{XP}\times \frac{BP}{PA} = 1\). Since \(PB=PA\), the latter expression further simplifies to \(\frac{AX}{XP}=\frac{YB}{PY}\). Add now \(1\) to both sides: \(\frac{AX+XP}{XP}=\frac{PY+YB}{PY}\), or \(\frac{PA}{XP}=\frac{PB}{PY},\space\)implying \(PX=PY\).

The above proof moved Hubert Shutrick to make the following observation:

The conics of the pencil through \(C\), \(D\), \(E\), \(F\) intersect the line \(AB\) in pairs of points in involution. Consider the degenerate members \(CD.EF\), \(CE.DF\), and \(l.l'\). \(P\) is a double point because of the first and so, if one of the pairs \(A,B\) and \(X,Y\) is symmetrical about \(P\), then so is the other.

Butterfly Theorem and Variants

  1. Butterfly theorem
  2. 2N-Wing Butterfly Theorem
  3. Better Butterfly Theorem
  4. Butterflies in Ellipse
  5. Butterflies in Hyperbola
  6. Butterflies in Quadrilaterals and Elsewhere
  7. Pinning Butterfly on Radical Axes
  8. Shearing Butterflies in Quadrilaterals
  9. The Plain Butterfly Theorem
  10. Two Butterflies Theorem
  11. Two Butterflies Theorem II
  12. Two Butterflies Theorem III
  13. Algebraic proof of the theorem of butterflies in quadrilaterals
  14. William Wallace's Proof of the Butterfly Theorem
  15. Butterfly theorem, a Projective Proof
  16. Areal Butterflies
  17. Butterflies in Similar Co-axial Conics
  18. Butterfly Trigonometry
  19. Butterfly in Kite
  20. Butterfly with Menelaus
  21. William Wallace's 1803 Statement of the Butterfly Theorem
  22. Butterfly in Inscriptible Quadrilateral
  23. Camouflaged Butterfly
  24. General Butterfly in Pictures
  25. Butterfly via Ceva
  26. Butterfly via the Scale Factor of the Wings
  27. Butterfly by Midline
  28. Stathis Koutras' Butterfly
  29. The Lepidoptera of the Circles
  30. The Lepidoptera of the Quadrilateral
  31. The Lepidoptera of the Quadrilateral II
  32. The Lepidoptera of the Triangle
  33. Two Butterflies Theorem as a Porism of Cyclic Quadrilaterals
  34. Two Butterfly Theorems by Sidney Kung
  35. Butterfly in Complex Numbers

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

71851987