William Wallace's 1803 Statement of the Butterfly Theorem
6 May 2015, Created with GeoGebra
At this point in time, there are two formulations of the Butterfly Theorem that have the distinction of having been thought at different times as the first mention of the theorem (but not of the Butterfly designation). An earlier formulation has been discovered recently, that predates the two and, perhaps surprisingly, is due to William Wallace himself.
I list the three in the temporal order of publication:
Sir William Wallace (question 121, The Gentlemen's Mathematical Companion, 1803):
If from any two points $B,E,$ in the circumference of a circle given in magnitude and position two right lines $BCA,EDA,$ be drawn cutting the circle in $C$ and $D,$ and meeting in $A;$ and from the point of intersection $A$ to the centre of the circle $AO$ be drawn, and the points $E,C;\;B,D$ joined, and produced to meet an indefinite perpendicular erected at $A$ on $AO;$ then will $FA$ be always equal $AF.$ Required the demonstration?
Sir William Herschel, in a letter to William Wallace, dated 7 April 1805
I have kept a little problem for you which a friend of mine has sent me who says he cannot find a solution of it. I mentioned to him that I had a friend who would probably help him to one. The problem is this. Given $AB$ the diameter of a circle. $CD$ a chord cutting it at right angles in $K.$ $EF,$ and $HG$ two other chords drawn any how through the point $K;$ and $HF,$ $EG$ chords joining the extremes of $EF, HG.$ Required to prove that $MK$ is equal to $LK.$

Rev. Thomas Scurr (question 1029, Gentlemen's Diary or Mathematical Repository, 1814):
Let $AB$ be any chord in a circle, through $I$ the middle point of which let two other chords be drawn, the former MIN, meeting the circle in $M,N,$ the latter $OIL,$ meeting the circle in $O,L;$ join the points $L,M,$ and $N,O,$ by right lines which cut the chord $AB$ in $P$ and $Q$ respectively; then is $AP=BQ.$ Required a demonstration.
Several observation can be made immediately (I shall refer to the three formulations as $W,$ $H,$ and $S,$ respectively):
The degree of their generality is the reverse of the temporal order: $W$ is more general than $H;$ $H$ is more general than $S.$
The diagram that accompanied $H$ (and implied by $S)$ is suggestive of the later designation as the Butterfly Theorem; much less so is the diagram that may be inferred from $W:$
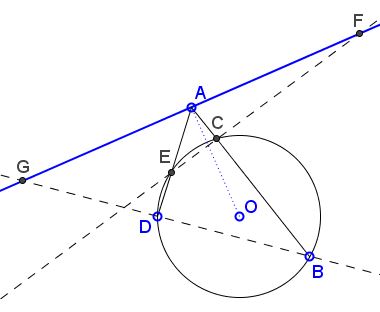
However, with point $A$ located within circle $(O),$ the relation between the three formulations becomes more transparent.
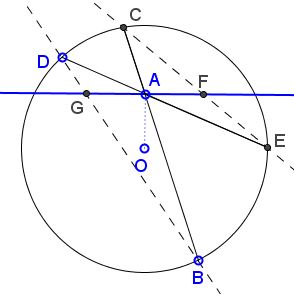
How do we observe the diminishing order of generality?
It is known that the line through the center of a circle is perpendicular to a chord if and only if it passes through the chord's midpoint. $W$ deals with a line perpendicular to another line through the center of the circle. $H$ takes the former to be a chord with named end points, although the latter play no visible role in the formulation. $S$ emphasizes the midpoint of a chord and, in addition, assigns specific role to its endpoints.
$H$ and $S$ are so formulated (and depicted) as to make an implicit assumption that the end points of the two chords that are being joined lie on different sides of the chord (line) that they are supposed to cross. This makes the intersections to be located on the chord, i.e., within the circle. $W$ appears indifferent to where the intersections may occur - within or without the circle. When the given line crosses the circle, $W$ allows for two possibilities, both of which are illustrated below:
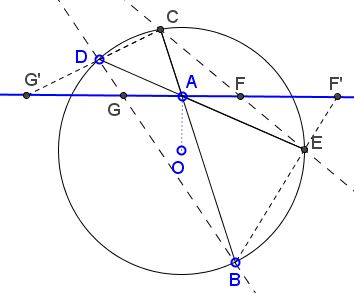
One is exactly the "butterfly" case, with the intersections $(G,F$) falling within the circle. The other pair, $(F',G')$ could probably suggest a two-leaf asymmetric propeller:

When the perpendicular to the line through the center of the circle does not cross the circle, the distinction between the two cases becomes meaningless, and this squarely places $W$ at the top of the order of generality.
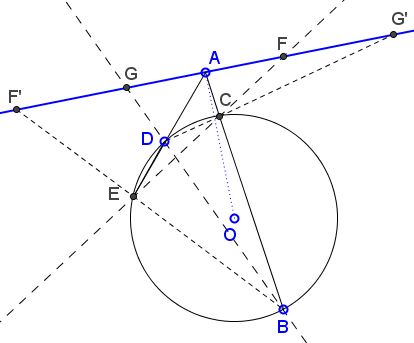
It is worth noting that all the proofs (algebraic, in particular) that do not directly appeal to the "butterfly" configuration of the traditional Butterfly theorem (e.g., ## 5, 9, 10) also do not distinguish between the two cases. All such proofs work for the general $W,$ the Wallace original formulation.
Three solutions to Wallace's question have been published in the 1804 issue of The Gentlemen's Mathematical Companion.
In conclusion, there may have been a reason why Hershel turned to Wallace with a problem related to the one Wallace posted earlier. No links have been yet discovered to the Scurr's posting.
Butterfly Theorem and Variants
- Butterfly theorem
- 2N-Wing Butterfly Theorem
- Better Butterfly Theorem
- Butterflies in Ellipse
- Butterflies in Hyperbola
- Butterflies in Quadrilaterals and Elsewhere
- Pinning Butterfly on Radical Axes
- Shearing Butterflies in Quadrilaterals
- The Plain Butterfly Theorem
- Two Butterflies Theorem
- Two Butterflies Theorem II
- Two Butterflies Theorem III
- Algebraic proof of the theorem of butterflies in quadrilaterals
- William Wallace's Proof of the Butterfly Theorem
- Butterfly theorem, a Projective Proof
- Areal Butterflies
- Butterflies in Similar Co-axial Conics
- Butterfly Trigonometry
- Butterfly in Kite
- Butterfly with Menelaus
- William Wallace's 1803 Statement of the Butterfly Theorem
- Butterfly in Inscriptible Quadrilateral
- Camouflaged Butterfly
- General Butterfly in Pictures
- Butterfly via Ceva
- Butterfly via the Scale Factor of the Wings
- Butterfly by Midline
- Stathis Koutras' Butterfly
- The Lepidoptera of the Circles
- The Lepidoptera of the Quadrilateral
- The Lepidoptera of the Quadrilateral II
- The Lepidoptera of the Triangle
- Two Butterflies Theorem as a Porism of Cyclic Quadrilaterals
- Two Butterfly Theorems by Sidney Kung
- Butterfly in Complex Numbers
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73580906
